Structure de données
from dataclasses import dataclass
from typing import Any
@dataclass
class Noeud:
"""Noeud d'un arbre binaire."""
valeur: Any = None
gauche: Any = None
droite: Any = None
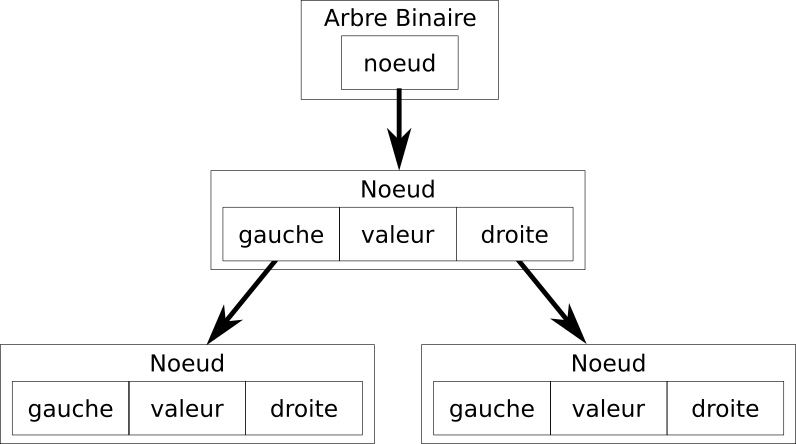
Noeud de départ
- Comment identifier le noeud de départ de l'arbre binaire ?
- On souhaite que chaque noeud ait la même représentation.
- On introduit un nouveau type,
ArbreBinaire, qui référence le noeud de départ. - Un
ArbreBinairen'a pas de valeur.
Noeud de départ identifié par l'ArbreBinaire
Structure de données
from dataclasses import dataclass
@dataclass
class ArbreBinaire:
"""Arbre binaire."""
noeud: Noeud = None
Exemple complet

Insertion et recherche dans un arbre binaire
Recherche : principe
- On part du noeud à la racine.
- On utilise la relation d'ordre pour savoir si on doit aller à gauche ou à droite.
- On descend dans l'arbre jusqu'à trouver la valeur ou ne plus avoir de descendants.
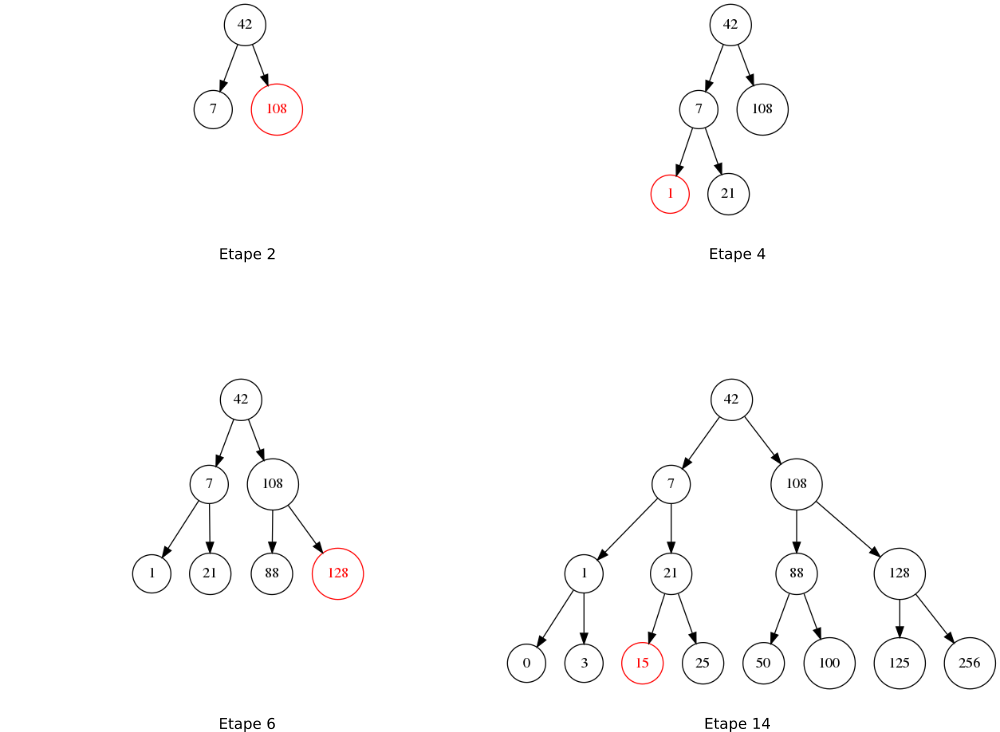
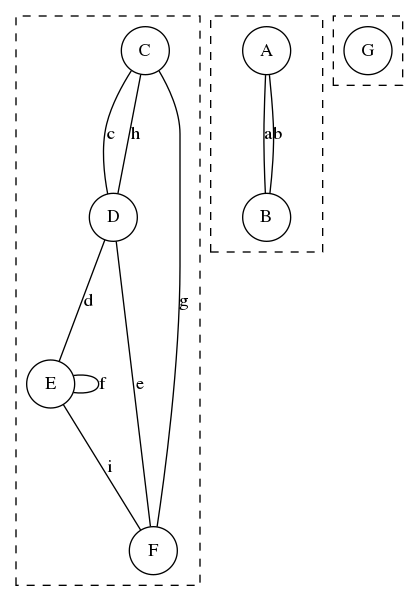
Illustration de la recherche
Valeur recherchée : 25

Etapes de recherche

Algorithme de recherche dans un arbre binaire
def trouve_valeur_dans_arbre_binaire(arbre, valeur):
"""Trouve une valeur dans l'arbre binaire."""
noeud = arbre.noeud
while noeud != None and noeud.valeur != valeur:
if valeur < noeud.valeur:
noeud = noeud.gauche
else:
noeud = noeud.droite
return noeud
Complexité
- Le nombre d'étapes est fonction de la profondeur
- Pour un arbre binaire équilibré de
- Pour un arbre binaire non-équilibré de
Insertion : principe
- Si le noeud racine est vide, la nouvelle valeur est positionnée à la racine.
- Sinon :
- On utilise la relation d'ordre pour descendre dans l'arbre.
- On créé un nouveau noeud dans un nouvel emplacement.
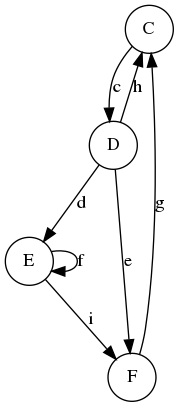
Illustration de l'insertion

Etapes d'insertion
Algorithme d'insertion
def insere_noeud_dans_arbre_binaire(arbre, valeur):
"""Insère un nouveau noeud dans un arbre binaire."""
if arbre.noeud == None:
arbre.noeud = Noeud(valeur=valeur)
return arbre.noeud
noeud = arbre.noeud
while noeud.valeur != valeur:
if valeur < noeud.valeur:
if noeud.gauche == None:
noeud.gauche = Noeud(valeur=valeur)
noeud = noeud.gauche
else:
if noeud.droite == None:
noeud.droite = Noeud(valeur=valeur)
noeud = noeud.droite
return noeud
 Problème
Problème 

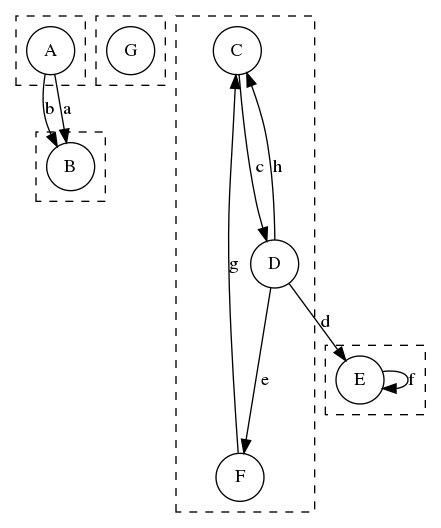
Etapes arbre binaire non-équilibré
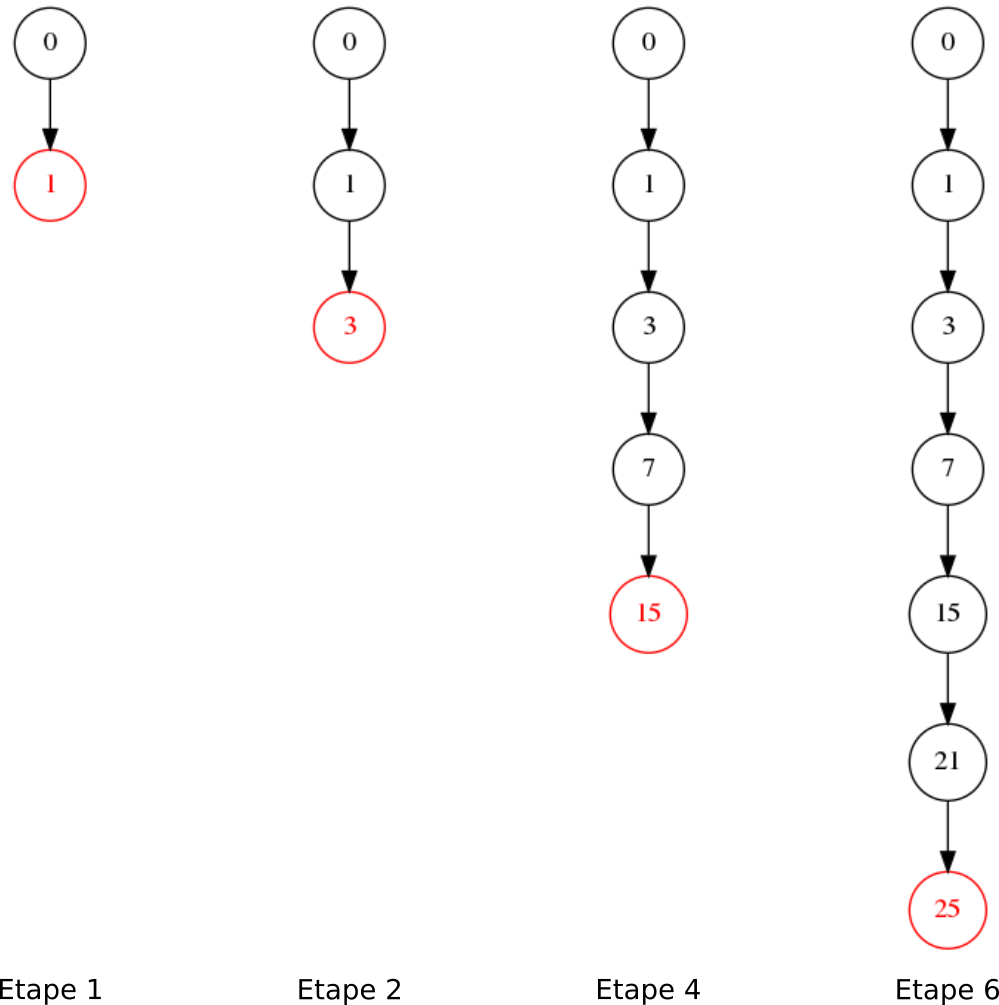
Arbre non-équilibré
- Si on insère toujours des valeurs à droite (ou à gauche), on obtient l'équivalent d'une liste chaînée.
- On perd alors l'équilibre de l'arbre, et la complexité d'insertion et de recherche augmente.
- La complexité passe de logarithmique à linéaire dans les 2 cas.
Solution : rééquilibrage
- Un arbre binaire rouge-noir (red-black binary search tree
) rééquilibre l'arbre à chaque insertion.
- Des rotations sont effectuées pour échanger des noeuds.
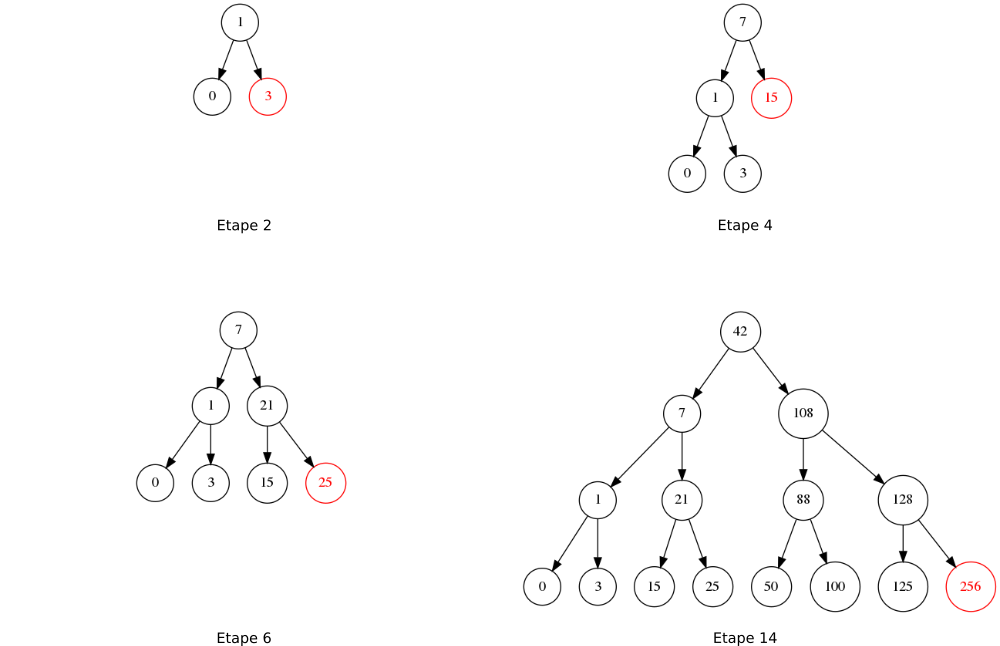
Illustration d'un arbre rouge-noir
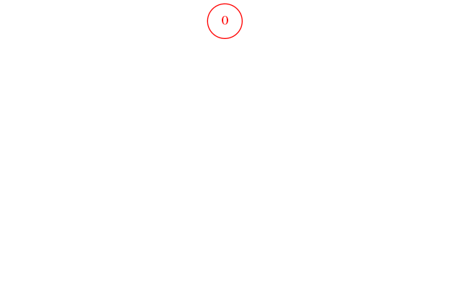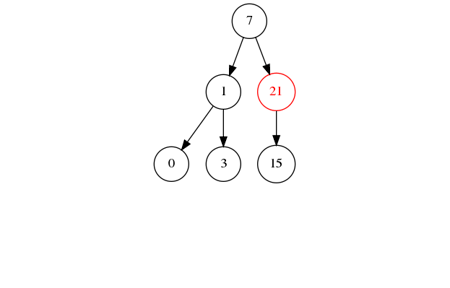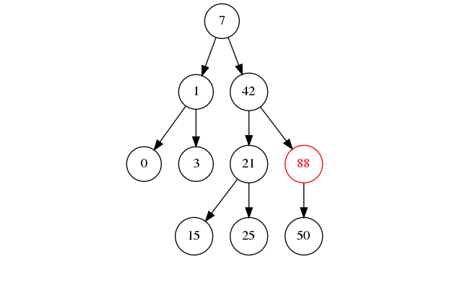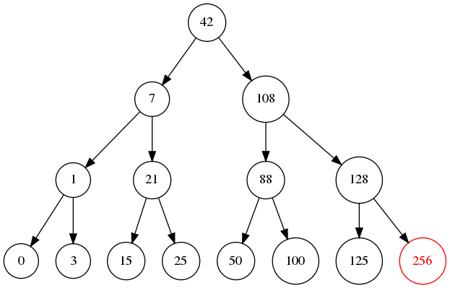
Etapes d'insertion dans un arbre rouge-noir
Complexité
Dans un arbre rouge-noir, la recherche et l'insertion sont en
Arbre de recherche N-aire
Généralisation
- Les arbres binaires ont de nombreuses propriétés intéressantes (complexité logarithmique).
- Toute hiérarchie ne peut être représentée avec un arbre binaire.
- Les arbres n-aires peuvent avoir
- Les descendants peuvent être une
list.
Illustration d'un arbre n-aire

Exemple avec une structure produit
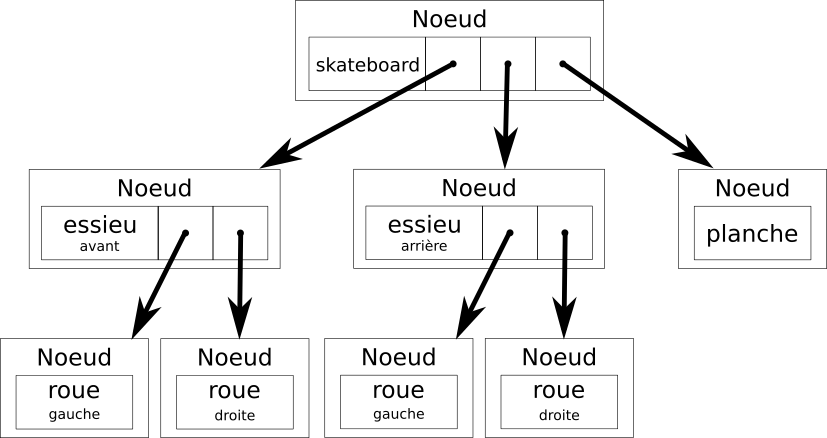
Structure de données
from dataclasses import dataclass, field
from typing import Any, List
@dataclass
class Noeud:
"""Noeud d'un arbre n-aire."""
valeur: Any = None
descendants: List = field(default_factory=list)
TP : Arbres binaires
TP : Arbres binaires
Discussion concernant les problèmes impliquant des graphes
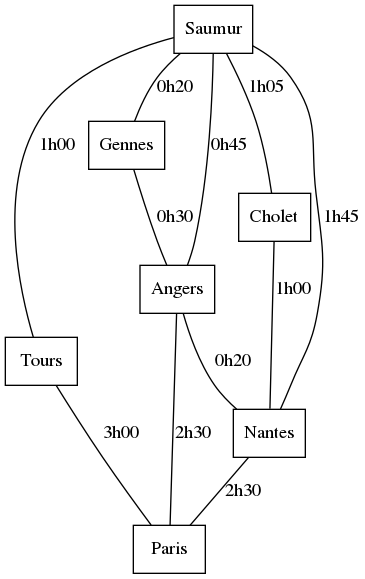
Trajet le plus rapide
Réseau
Réseau social

Introduction à la théorie des graphes
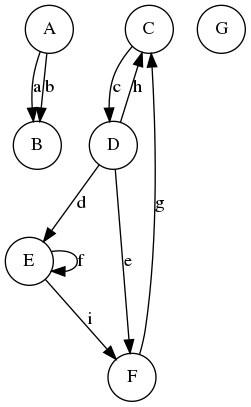
Graphe orienté (1/2)
- Un graphe orienté (directed graph ou digraph
) est caractérisé par :
- un ensemble
).
- un ensemble
).
- un ensemble
Graphe orienté (2/2)
- Chaque arc a une origine (source
) et un but (target
).
- On note
Exemple de graphe orienté
Graphe non-orienté (1/2)
- Un graphe non-orienté (undirected graph
) ou graphe symétrique est caractérisé par :
- un ensemble
- un ensemble
- un ensemble
Graphe non-orienté (2/2)
- Chaque arête a 2 extrémités (éventuellement confondues).
- Tout graphe orienté admet un graphe non-orienté sous-jacent.
- Le graphe sous-jacent est composé de l'ensemble des arêtes correspondant aux arcs du digraph.
Exemple de graphe non-orienté
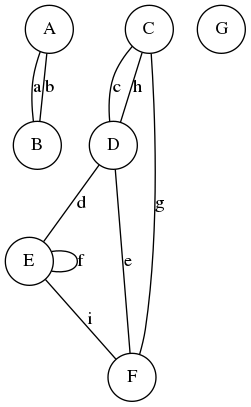
Graphe partiel
- On peut restreindre un graphe (orienté ou non) à une partie de ses arcs ou arêtes.
- Il s'agit d'un graphe partiel.
 |
 |
|---|---|
| Graphe orienté |
Graphe induit
- On peut restreindre un graphe (orienté ou non) à une partie de ses sommets.
- Il s'agit d'un graphe induit (ou sous-graphe).
 |
 |
|---|---|
| Graphe orienté |
Graphe simple
- Un graphe est dit simple s'il existe au plus un arc (ou arête) entre une origine et un but.
- Dans ce cas, un arc
 |
 |
|---|---|
| Graphe orienté |
Graphe antisymétrique
- Un graphe orienté simple est dit antisymétrique si, pour tout arc
 |
 |
|---|---|
| Graphe simple |
Chemin
- Un chemin d'un graphe orienté est une suite d'arcs.
- L'origine d'un arc est le but de l'arc prédécédent.
- Le chemin
 |
|---|
| Chemin |
Chemin simple
- Un chemin simple ne passe pas 2 fois par le même arc.
 |
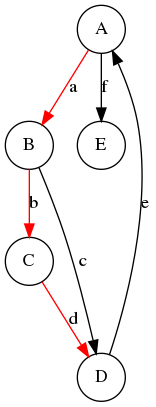 |
|---|---|
| Chemin non simple | Chemin simple |
Cycle (ou circuit)
- Dans un graphe orienté, un circuit est un chemin dont l'origine et le but sont confondus.
- Dans un graphe non-orienté, un cycle est un chemin dont l'origine et le but sont confondus.
 |
 |
|---|---|
| Circuit | Cycle dans le graphe sous-jacent |
Circuit élémentaire
- Un circuit est élémentaire s'il ne passe pas 2 fois par le même sommet (sauf l'origine et le but).
 |
 |
|---|---|
| Circuit non élémentaire | Circuit élémentaire |
Boucle
- Une boucle est un circuit composé d'un seul arc.

DAG (Directed Acyclic Graph  )
)
- Un DAG est un graphe orienté sans circuit.
- Ce type de graphe est courant.
 |
 |
|---|---|
| DAG |
Fermeture transitive - définition (1/2)
- La fermeture transitive (ou clôture transitive) d'un graphe simple
- Pour tout couple de sommets
Fermeture transitive - exemple (2/2)
 |
 |
|---|---|
| Graphe simple | Fermeture transitive |
Graphe connexe
- Un graphe non-orienté est connexe s'il existe un chemin entre chaque couple de sommets de ce graphe.
 |
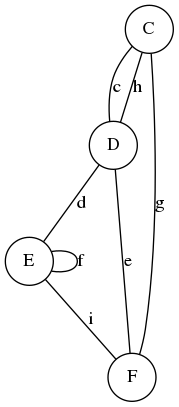 |
|---|---|
| Graphe non connexe | Graphe connexe |
Composante connexe
- La composante connexe d'un sommet
Graphe fortement connexe
- Un graphe orienté est fortement connexe s'il existe un chemin entre chaque couple de sommets de ce graphe.
 |
 |
|---|---|
| Graphe non fortement connexe | Graphe fortement connexe |
Composante fortement connexe
- La composante fortement connexe d'un sommet
Arbre
- En théorie des graphes, un arbre est un graphe non-orienté simple, connexe et sans cycle.
- Deux sommets quelconques ne sont reliés que par un unique chemin.
- Le nombre d'arcs est relié au nombre de sommets par la relation :
Forêt
- Une fôret est un graphe non-orienté dont les composantes connexes sont des arbres.
Arborescence
- Une arborescence est un graphe orienté possédant un sommet privilégié, la racine.
- Il existe un unique chemin de la racine à tout autre sommet.
- La racine n'a pas de prédécesseur.
- Tout autre sommet a un unique prédécesseur : son parent.
Représentations des graphes
Plusieurs représentations
- Il existe plusieurs manières de représenter un graphe en informatique.
- Chaque représentation a des avantages et des inconvénients.
- Un type de représentation ne convient pas à tous les types de graphes.
Liste de listes d'arcs (1/4)
- Le graphe orienté peut être caractérisé par une liste de sommets.
- Chaque sommet est caractérisé par une liste d'arcs et une éventuelle étiquette.
Liste de listes d'arcs (2/4)
- sommet 0 :
- sommet 1 :
- sommet 2 :
- sommet 3 :
- sommet 4 :
Liste de listes d'arcs (3/4)
G = [
[1], # 0 -> 1
[3, 4], # 1 -> 3, 1 -> 4
[4], # 2 -> 4
[0, 2], # 3 -> 0, 3 -> 2
[] # aucun
]
Liste de listes d'arcs (4/4)
- Il est possible également de représenter un graphe non-orienté en dupliquant les arcs pour former les arêtes.
- Avantages : simplicité de mise à jour et de parcours.
- Inconvénients : difficulté d'obtention de la liste des prédécesseurs sans dupliquer les arcs (pour avoir les arcs "retour").
Matrice d'adjacence (1/6)
- Un graphe simple à
- L'élément
Matrice d'adjacence (2/6)
| sommets | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| sommet 0 : | 0 | 1 | 0 | 0 | 0 |
| sommet 1 : | 0 | 0 | 0 | 1 | 1 |
| sommet 2 : | 0 | 0 | 0 | 0 | 1 |
| sommet 3 : | 1 | 0 | 1 | 0 | 0 |
| sommet 4 : | 0 | 0 | 0 | 0 | 0 |
Matrice d'adjacence (3/6)
Matrice d'adjacence (4/6)
M = [
[0, 1, 0, 0, 0],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 1],
[1, 0, 1, 0, 0],
[0, 0, 0, 0, 0]
]
Matrice d'adjacence (5/6)
- Si les arcs sont étiquettés, on peut utiliser ce type de représentation :
M = [
[None, "a", None, None, None],
[None, None, None, "b", "c"],
[None, None, None, None, "e"],
[ "f", None, "g", None, None],
[None, None, None, None, None]
]
Matrice d'adjacence (6/6)
- Avantages : représentation compacte, rapidité des recherches (notamment des prédécesseurs) et simplicité des algorithmes de calcul.
- Inconvénients : nombreux zéros dans la matrice (information "inutile"), redondance des informations pour les graphes non-orientés, ne convient que pour les graphes simples.
Matrice d'incidence (1/5)
- Un graphe non-orienté à
- L'élément
- Une colonne de cette matrice comporte donc toujours deux éléments à 1 : les 2 extrémités de l'arête.
Matrice d'incidence (2/5)
| arêtes | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| sommet 0 : | 1 | 0 | 0 | 0 | 1 | 0 |
| sommet 1 : | 1 | 1 | 1 | 0 | 0 | 0 |
| sommet 2 : | 0 | 0 | 0 | 1 | 0 | 1 |
| sommet 3 : | 0 | 1 | 0 | 0 | 1 | 1 |
| sommet 4 : | 0 | 0 | 1 | 1 | 0 | 0 |
Matrice d'incidence (3/5)
Matrice d'incidence (4/5)
M = [
[1, 0, 0, 0, 1, 0],
[1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 1],
[0, 0, 1, 1, 0, 0]
]
Matrice d'incidence (5/5)
- Avantages : informations non redondantes pour les graphes non-orientés, représentation compacte, rapidité des recherches.
- Inconvénients : nombreux zéros dans la matrice (information "inutile"), certaines opérations matricielles ne s'appliquent pas.
Parcours en profondeur
Depth-First Search 
Intérêt
- Tous les algorithmes d'analyse de graphes ont besoin de parcourir les graphes.
- Les algorithmes de parcours constituent le socle de ces algorithmes plus avancés.
Principe
- On parcourt chaque sommet du graphe.
- Les ordres de parcours dépendent de l'ordre des sommets et de l'ordre des successeurs de chaque sommet.
- Il existe 2 algorithmes principaux de parcours d'un graphe :
- le parcours en profondeur,
- le parcours en largeur.
Parcours en profondeur
- Le parcours en profondeur (DFS - Depth-First Search
) consiste à aller aussi profondément que possible dans le graphe à chaque étape.
- On visite le 1er successeur du 1er sommet, puis son 1er successeur, puis son 1er successeur, etc.
- On remonte ensuite la chaîne pour visiter le 2e successeur du dernier sommet visité, puis le 1er successeur de ce nouveau sommet, etc.
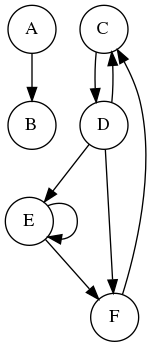
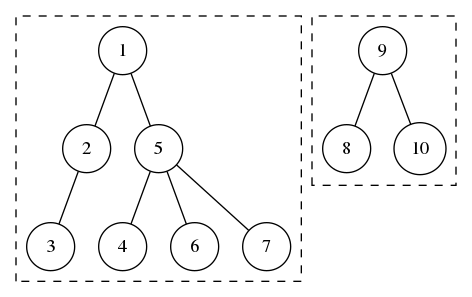
Exemple avec une arborescence

Ordre de visite : 0, 1, 4, 10, 11, 5, 6, 2, 7, 12, 13, 14, 3, 8, 9.
Exemple avec un graphe simple

Ordre de visite : 0, 1, 3, 2, 4.
Exemple avec un graphe non-connexe

Ordre de visite : 0, 3, 2, 7, 12, 11, 6, 13, 14, 9, 10, 8, 4, 1, 5, 11, 15, 16, 17, 18, 19.
Algorithme DFS (récursif)
def parcours_en_profondeur(m, f):
"""Applique la fonction f à chaque sommet du graphe.
m - matrice d'adjacence.
f - fonction prenant un sommet en argument.
"""
def parcours_successeurs(m, s, f, marque):
"""Traitement récursif."""
if s not in marque:
marque.append(s)
f(s)
suivants = successeurs(m, s)
for suivant in suivants:
parcours_successeurs(m, suivant, f, marque)
marque = []
for s in range(len(m)):
parcours_successeurs(m, s, f, marque)
Complexité
- Chaque sommet est visité.
- Or, les sommets déjà visités sont marqués pour ne pas être traités à nouveau.
- Donc chaque sommet est visité exactement 1 fois.
- Chaque arc d'origine est visité 1 fois.
- Dans le pire cas, le nombre maximal d'opérations sera limité soit par le nombre de sommets, soit par le nombre d'arcs.
- La complexité est donc
Parcours en largeur
Breadth-First Search 
Parcours en largeur
- Le parcours en largeur (BFS - Breath-First Search) consiste à visiter d'abord tous les successeurs directs.
- Une fois que tous les successeurs directs ont été visités, on passe aux successeurs du 1er successeur, etc.
Exemple avec une arborescence
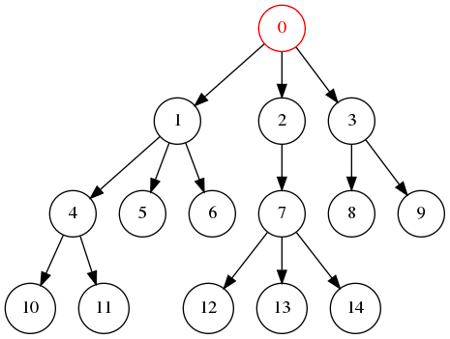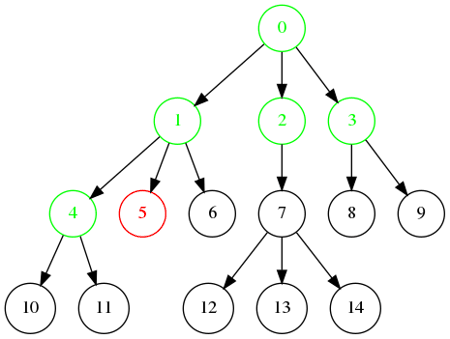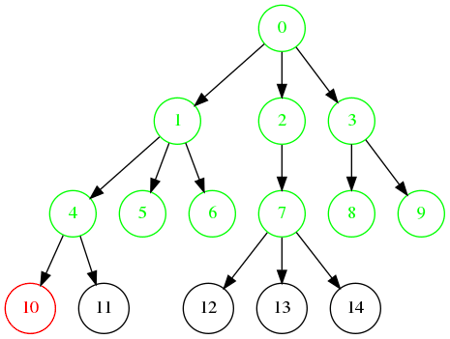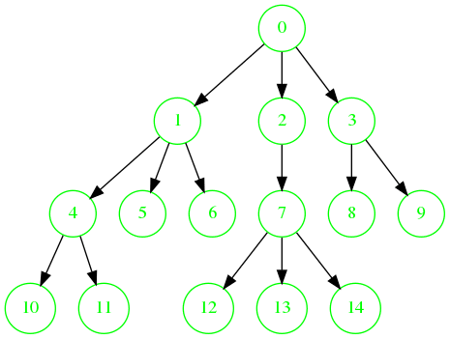
Ordre de visite : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
Exemple avec un graphe simple
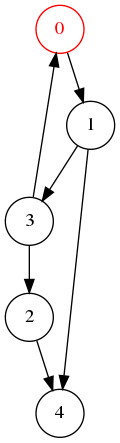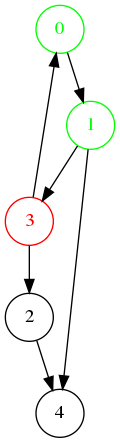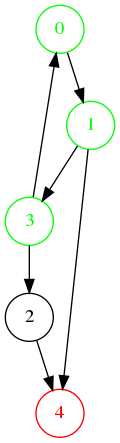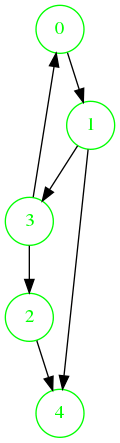
Ordre de visite : 0, 1, 3, 4, 2.
Exemple avec un graphe non-connexe

Ordre de visite : 0, 3, 4, 2, 8, 9, 1, 5, 11, 7, 6, 12, 13, 14, 10, 15, 16, 18, 17, 19.
Algorithme BFS
def parcours_en_largeur(m, f):
"""Applique la fonction f à chaque sommet du graphe.
m - matrice d'adjacence.
f - fonction prenant un sommet en argument.
"""
marque = [] # On ne souhaite pas traiter plusieurs fois un sommet
queue = [] # On utilise une queue pour traiter d'abord les plus proches
for s in range(len(m)): # Visite chaque sommet pour les graphes non-connexes
if s not in marque: # Evite de traiter 2 fois un sommet
marque.append(s) # Marque le sommet courant à traiter
queue.append(s) # Empile dans la queue des sommets à traiter
while len(queue) != 0: # Tant que la queue est non vide
s_i = queue.pop(0) # On prend le 1er sommet
f(s_i) # On traite s_i
suivants = successeurs(m, s_i) # On prend les successeurs
for suivant in suivants: # On parcourt les successeurs
if suivant not in marque: # Les successeurs non marqués
marque.append(suivant) # sont marqués
queue.append(suivant) # et empilés.
Complexité
- On parcourt chaque sommet exactement une fois.
- La complexité est en
Identification d'un cycle
Intérêt
- De nombreux algorithmes ne fonctionnent qu'avec des graphes acycliques.
- Il faut donc pouvoir identifier si un cycle existe avant d'utiliser de tels algorithmes.
Principe
- Pour identifier un cycle, on peut utiliser le parcours en profondeur.
- On ajoute un argument à la fonction récursive pour identifier le chemin courant.
- Si on cherche à revisiter un sommet dans ce chemin, on a identifier un cycle.
- Il ne reste plus qu'à retourner ce cycle.
Algorithme
def cherche_cycle_en_profondeur(m, s, marque, chemin):
"""Recherche en profondeur un cycle.
m - matrice d'adjacence.
s - sommet à visiter.
marque - liste de sommets marqués.
chemin - chemin jusqu'à s.
"""
cs = chemin + [s] # On construit le nouveau chemin cs
if s in chemin: # Si un cycle est identifié dans le chemin,
return cs # on le renvoie.
if s not in marque: # Parcours en profondeur
marque.append(s) # On marque le sommet s
suivants = successeurs(m, s) # On prend les successeurs de s
for suivant in suivants: # On vérifie les sous-chemins
cycle = cherche_cycle_en_profondeur(m, suivant, marque, cs)
if cycle != None: # Si un cycle a été identifié dans
return cycle # un sous-chemin, on le renvoie.
return None # Pas de cycle identifié
Interface
def identifie_cycle(m):
"""Retourne le premier cycle identifié ou None."""
marque = []
for s in range(len(m)):
cycle = identifie_cycle_dans_chemin(m, s, marque, [])
if cycle != None:
return cycle
return None
Exemple
cycle = identifie_cycle(G)
print(cycle)
[0, 1, 3, 0]
Complexité
- La complexité est la même que pour le parcours en profondeur :
Graphe pondéré : représentation
Principe
- On associe un poids à chaque arc ou arête.
- Le poids est un nombre flottant.
- Le poids peut donc être positif ou négatif.
- Exemple :
- un sommet peut représenter une ville,
- une arête pondérée peut représenter le temps de trajet entre ces villes.
Liste de listes de listes (1/3)
- Pour un graphe non-pondéré, on pouvait utiliser une liste de listes.
- Chaque sous-liste représente les successeurs d'un sommet.
- Pour ajouter les poids, on ajoute une dimension.
- On obtient la hiérarchie suivante :
- liste de sommets
- liste de successeurs
- liste des labels et poids
- liste de successeurs
- liste de sommets
Liste de listes de listes (2/3)
G = [
[ # 0 -> 1 (poids = 42)
[1, 42]
],
[ # 1 -> 3 (poids = 21), 1 -> 4 (poids = -56.7)
[3, 21],
[4, -56.7]
],
[ # 2 -> 4 (poids = 7)
[4, 7]
],
[ # 3 -> 0 (poids = 3.14), 3 -> 2 (poids = -8)
[0, 3.14],
[2, -8]
],
[] # aucun
]
Liste de listes de listes (3/3)
- Avantages : évolution simple d'une représentation non-pondérée.
- Inconvénient : mêmes inconvénients qu'avec une liste de listes, plus difficile à comprendre et à maintenir.
Matrice d'adjacence (1/5)
- On peut représenter un graphe orienté valué à
Matrice d'adjacence (2/5)
| sommets | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| sommet 0 : | 42 | ||||
| sommet 1 : | 21 | -56.7 | |||
| sommet 2 : | 7 | ||||
| sommet 3 : | 3.14 | -8 | |||
| sommet 4 : |
Matrice d'adjacence (3/5)
Matrice d'adjacence (4/5)
M = [
[None, 42, None, None, None],
[None, None, None, 21, -56.7],
[None, None, None, None, 7 ],
[3.14, None, -8, None, None],
[None, None, None, None, None]
]
Matrice d'adjacence (5/5)
- Avantages : mêmes avantages qu'une matrice d'adjacence non-pondérée.
- Inconvénients : mêmes inconvénients qu'une matrice d'adjacence non-pondérée (mais pas d'inconvénient supplémentaire contrairement à la liste de listes de listes).
Structures de données (1/3)
@dataclass
class Sommet:
"""Sommet d'un graphe."""
label: int = 0
@dataclass
class Arc:
"""Arc d'un graphe orienté"""
origine: int = 0
but: int = 0
poids: float = 0.
@dataclass
class GraphePondere:
"""Graphe orienté pondéré."""
sommets: List = field(default=list)
arcs: List = field(default=list)
Structures de données (2/3)
s0 = Sommet(0)
s1 = Sommet(1)
s2 = Sommet(2)
s3 = Sommet(3)
s4 = Sommet(4)
a0 = Arc(origine=0, but=1, poids=42)
a1 = Arc(origine=1, but=3, poids=21)
a2 = Arc(origine=1, but=4, poids=-56.7)
a3 = Arc(origine=2, but=4, poids=7)
a4 = Arc(origine=3, but=2, poids=-8)
a5 = Arc(origine=3, but=0, poids=3.14)
G = GraphePondere(sommets=[s0, s1, s2, s3, s4],
arcs=[a0, a1, a2, a3, a4, a5])
Structures de données (3/3)
- Avantages : Les données sont plus structurées qu'avec une liste de liste de listes.
- Inconvénients : On a les mêmes inconvénients qu'avec une liste de listes.
Plus court chemin
Principe
- La recherche du chemin le plus court dans un graphe pondéré est un problème classique.
- Le poids d'un chemin est égal à la somme des poids des arcs sur ce chemin.
- Il existe différents algorithmes pour résoudre ce problème.
- Nous étudierons uniquement l'algorithme Bellman-Ford dans ce cours.
Bellman-Ford - principe (1/2)
- L'algorithme Bellman-Ford permet de construire un arbre des plus courts chemins (SPT - shortest path tree
).
- Cet algorithme considère les graphes orientés pondérés sans circuit négatif.
Bellman-Ford - principe (2/2)
- Cet algorithme part d'un sommet
- Au départ, on évalue toutes les distances de
- On effectue, sur le principe, un parcours en largeur pour réévaluer à chaque étape la distance minimale de
- L'implémentation suivante utilise une matrice d'adjacence.
Bellman-Ford - algorithme (1/4)
def adjacents(m, s):
"""Renvoie les arcs adjacents à s dans m."""
adj = []
for j in range(len(m[s])):
if m[s][j] != None:
adj.append(Arc(origine=s, but=j, poids=m[s][j]))
return adj
Bellman-Ford - algorithme (2/4)
def recalcule_bellman_ford(m, s, dist_a, arc_vers, queue):
"""Recalcule la distance minimale en considérant les successeurs de s.
m - matrice d'adjacence pondérée.
s - sommet dans les successeurs sont considérés.
dist_a - liste des distances minimales aux autres sommets.
arc_vers - liste des arcs conservés pour aller à un sommet donné.
queue - queue pour le parcours en largeur.
"""
adj = adjacents(m, s)
for arc in adj:
w = arc.but
if dist_a[w] == None or dist_a[w] > dist_a[s] + arc.poids:
dist_a[w] = dist_a[s] + arc.poids
arc_vers[w] = arc
if w not in queue:
queue.append(w)
Bellman-Ford - algorithme (3/4)
def bellman_ford_impl(m, s):
"""Implémentation de Bellman-Ford sans gestion de cycles négatifs.
m - matrice d'adjacence pondérée.
s - sommet de départ.
Renvoie la liste des distances aux autres sommets et la liste des
arcs constituant les plus courts chemins.
"""
dist_a = [None for _ in range(len(m))] # distances à l'infini
dist_a[s] = 0 # distance à lui-même
arc_vers = [None for _ in range(len(m))] # résultat
queue = [s]
while len(queue) != 0:
v = queue.pop(0)
recalcule_bellman_ford(m, v, dist_a, arc_vers, queue)
return dist_a, arc_vers
Bellman-Ford - algorithme (4/4)
def bellman_ford(m, s):
"""Renvoie une matrice d'adjacence correspondant au shortest path
tree (SPT) et la liste des distances minimales."""
dist_a, arc_vers = bellman_ford_impl(m, s)
spt = [[None for _ in range(len(m))] for _ in range(len(m))]
for arc in arc_vers:
if arc != None:
spt[arc.origine][arc.but] = arc.poids
return spt, dist_a
Note : Nous omettons la recherche de circuit négatif pour simplifier l'implémentation.
Bellman-Ford - exemple (1/2)
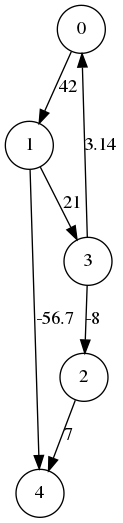 |
 |
|---|---|
| Graphe pondéré | Arbre de distances minimales pour |
Coûts = [0, 42, 55, 63, -14.7]
Bellman-Ford - exemple (2/2)
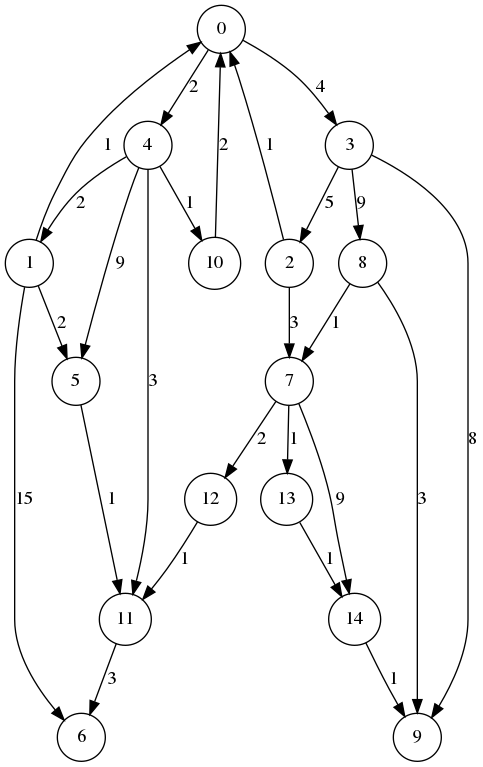 |
 |
|---|---|
| Graphe pondéré | Arbre de distances minimales pour |
Coûts = [0, 4, 9, 4, 2, 6, 8, 12, 13, 12, 3, 5, 14, 13, 14]
Complexité
- La complexité de l'algorithme Bellman-Ford est en
- Cet algorithme est applicable dans de nombreux cas en pratique, sa complexité est correcte et son implémentation est relativement simple.
- L'algorithme de Dijkstra offre une meilleure complexité en
Recherche de chemin critique
Problème d'ordonnancement
- Un problème d'ordonnancement simple est caractérisé par un ensemble de tâches à exécuter.
- Chaque tâche a une durée déterminée.
- Chaque tâche a des contraintes de précédence : pour exécuter une tâche, ses prédecesseurs doivent être exécutés préalablement.
Caractérisation des tâches
- Tâche critique : son exécution ne peut être allongée ou différée sans allonger la durée du projet.
- Marge libre d'une tâche : temps maximal dont cette tâche peut être allongée ou différée sans retarder le projet, indépendamment des autres tâches.
Méthode PERT (1/2)
- La méthode PERT (Project Evaluation and Review Technique
) utilise un DAG (graphe orienté acyclique) pour représenter et solutionner un problème d'ordonnancement.
- Le sommet début est à la racine du graphe.
- Le sommet fin marque la fin du projet.
Méthode PERT (2/2)
- Chaque tâche est représentée par un arc pondéré par la durée de la tâche.
- Les relations de précédences sont représentées par des arcs de poids nul.
Exemple (1/3)
| Tâches | Durée (jours) | Prédécesseurs |
|---|---|---|
| T1 : Architecturer Solution | 2 | |
| T2 : Configurer Serveurs | 1 | |
| T3 : Configurer BD | 3 | |
| T4 : Plan de Tests | 2 | |
| T5 : Coder Front End | 5 | T1 |
| T6 : Coder Backend | 7 | T1, T2, T3 |
| T7 : Tests | 3 | T4, T5, T6 |
Exemple (2/3)

Exemple (3/3)
NA = None # Non Applicable
M = [
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
[NA, 0, 0, 0, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA], # 0
[NA, NA, NA, NA, 2, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 1
[NA, NA, NA, NA, NA, 1, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 2
[NA, NA, NA, NA, NA, NA, 3, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 3
[NA, NA, NA, NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA, NA, NA], # 4
[NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA, NA, NA, NA], # 5
[NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA, NA, NA, NA], # 6
[NA, NA, NA, NA, NA, NA, NA, NA, NA, 5, NA, NA, NA, NA, NA, NA], # 7
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 7, NA, NA, NA, NA, NA], # 8
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 9
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 10
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 2, NA, NA, NA], # 11
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 12
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 3, NA], # 13
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0], # 14
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA] # 15
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
]
Chemin critique
- Un chemin critique est un chemin de poids maximal allant de
débutàfin. - Il peut y avoir plusieurs chemins critiques.
- Toute tâche sur un chemin critique est une tâche critique.
- Nous cherchons à trouver un chemin critique.
Exemple de chemin critique
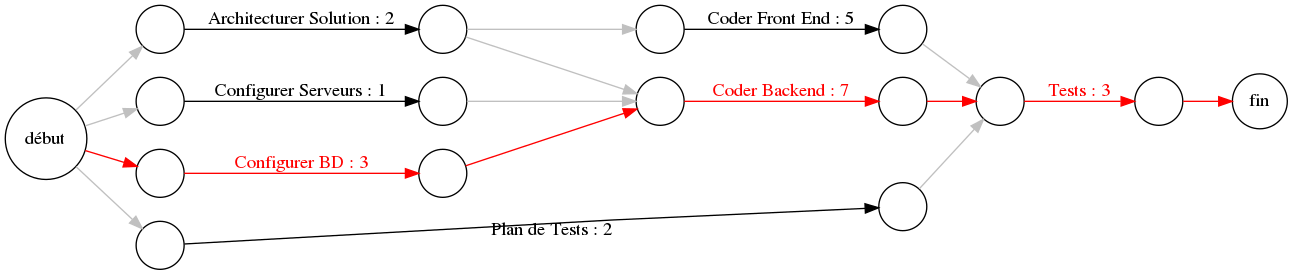
Plus long chemin (1/2)
- Un chemin critique est donc un plus long chemin de
débutàfin. - Il est possible d'utiliser un algorithme de plus court chemin pour calculer un plus long chemin.
- L'astuce consiste à créer un DAG équivalent avec des poids négatifs.
- Un poids de
2devient donc un poids de-2par exemple.
Plus long chemin (2/2)
- Avec des poids négatifs, le plus court chemin va trouver le plus long chemin en valeur absolue.
- Comme PERT utilise un DAG, on va pouvoir utiliser Bellman-Ford.
- En effet, un DAG ne contient pas de circuit et par conséquent, il ne contient pas de circuit négatif.
Exemple de plus long chemin
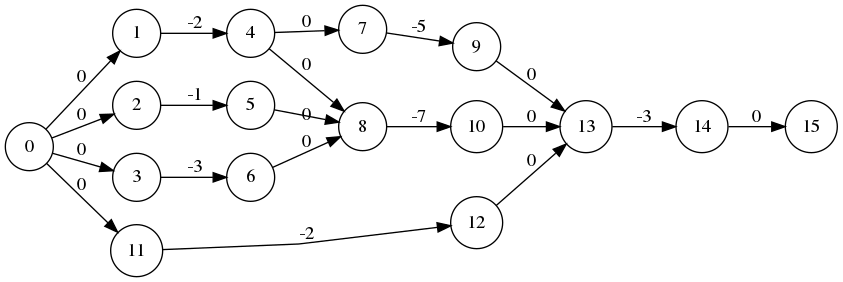
Algorithme (1/3)
def oppose_poids(m):
"""Renvoie une matrice d'adjacence dont les poids sont opposés."""
resultat = []
for i in range(len(m)):
ligne = []
for j in range(len(m)):
if m[i][j] == None:
ligne.append(None)
else:
ligne.append(-m[i][j])
resultat.append(ligne)
return resultat
Algorithme (2/3)
def chemin_vers(s, dist_a, arc_vers):
"""Renvoie le chemin vers le sommet s."""
if dist_a[s] == None:
return None
chemin = []
arc = arc_vers[s]
while arc != None:
predecesseur = arc.origine
chemin.insert(0, predecesseur)
arc = arc_vers[predecesseur]
return chemin
Algorithme (3/3)
def chemin_critique(m):
"""Renvoie le chemin critique en utilisant PERT.
Utilise Bellman-Ford sur l'opposé de la matrice d'adjacence.
La matrice d'adjacence doit représenter un DAG.
Par convention, le début est supposé être le 1er sommer, et
la fin est supoosée être le dernier sommet.
"""
# Construit une matrice d'adjacence avec les poids opposés
m_p = oppose_poids(m)
# Calcule l'arbre des plus courts chemins
dist_a, arc_vers = bellman_ford_impl(m_p, 0)
# Le chemin vers la fin est le chemin critique
fin = len(m) - 1
chemin = chemin_vers(fin, dist_a, arc_vers)
return chemin
Exemple
c = chemin_critique(M)
print(c)
[0, 3, 6, 8, 10, 13, 14]
Complexité
- On utilise Bellman-Ford, et donc la complexité est similaire :
