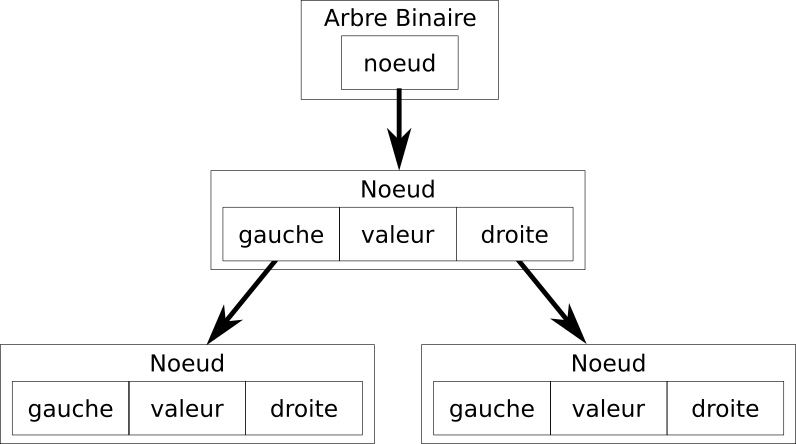
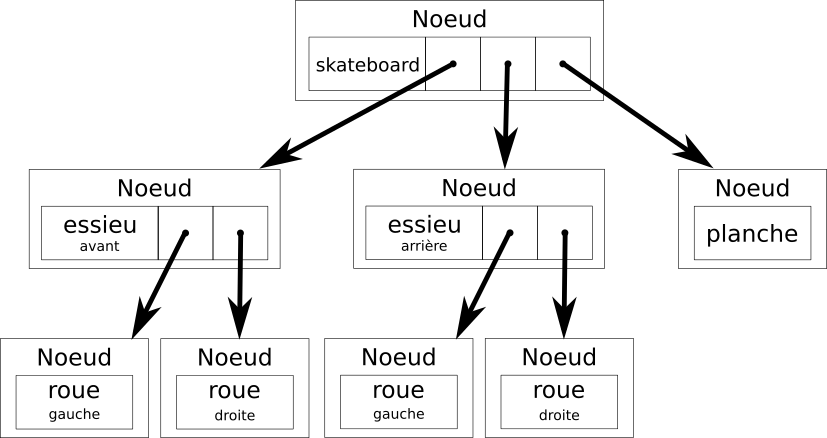
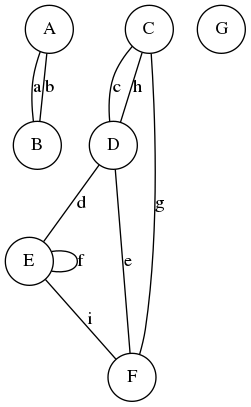
Noeud de départ identifié par l'ArbreBinaire
from dataclasses import dataclass
from typing import Any
@dataclass
class Noeud:
"""Noeud d'un arbre binaire."""
valeur: Any = None
gauche: Any = None
droite: Any = None
ArbreBinaire, qui référence le noeud de départ.ArbreBinaire n'a pas de valeur.ArbreBinaire
from dataclasses import dataclass
@dataclass
class ArbreBinaire:
"""Arbre binaire."""
noeud: Noeud = None



def trouve_valeur_dans_arbre_binaire(arbre, valeur):
"""Trouve une valeur dans l'arbre binaire."""
noeud = arbre.noeud
while noeud != None and noeud.valeur != valeur:
if valeur < noeud.valeur:
noeud = noeud.gauche
else:
noeud = noeud.droite
return noeud

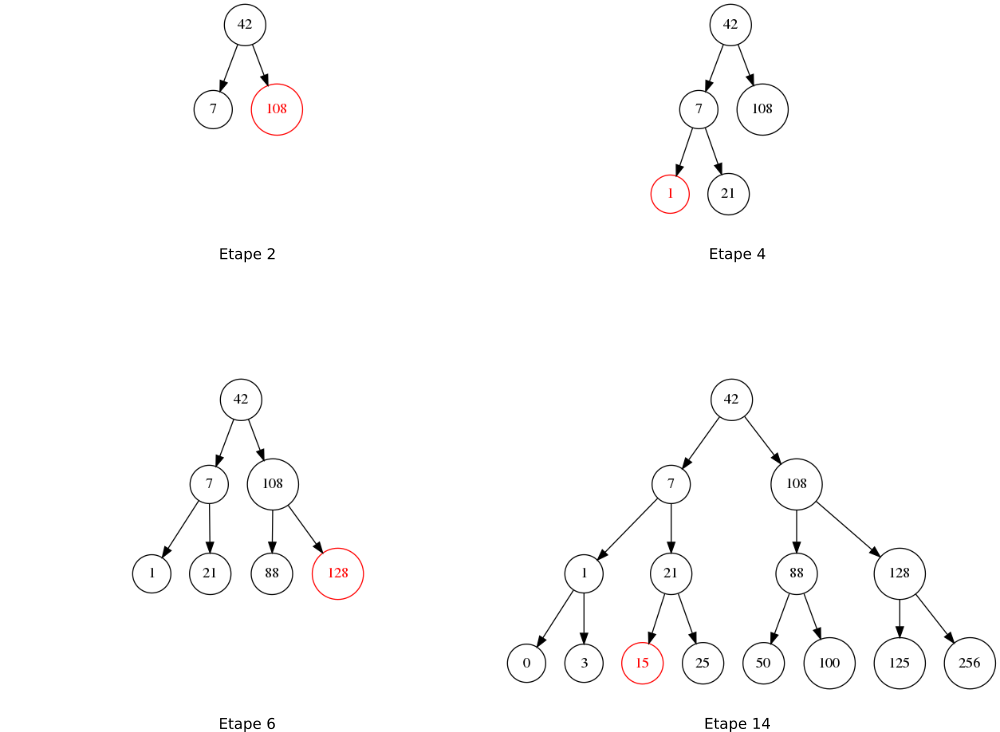
def insere_noeud_dans_arbre_binaire(arbre, valeur):
"""Insère un nouveau noeud dans un arbre binaire."""
if arbre.noeud == None:
arbre.noeud = Noeud(valeur=valeur)
return arbre.noeud
noeud = arbre.noeud
while noeud.valeur != valeur:
if valeur < noeud.valeur:
if noeud.gauche == None:
noeud.gauche = Noeud(valeur=valeur)
noeud = noeud.gauche
else:
if noeud.droite == None:
noeud.droite = Noeud(valeur=valeur)
noeud = noeud.droite
return noeud
 Problème
Problème 

 ) rééquilibre l'arbre à chaque insertion.
) rééquilibre l'arbre à chaque insertion.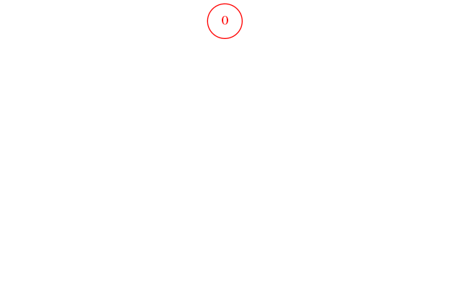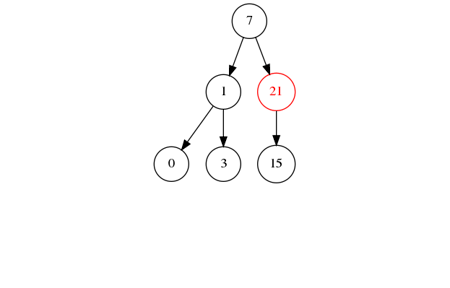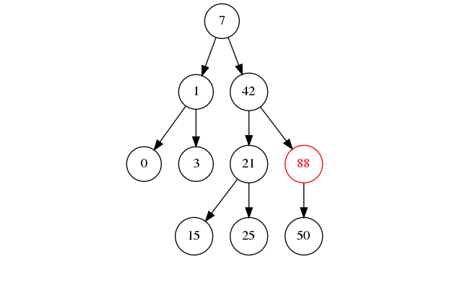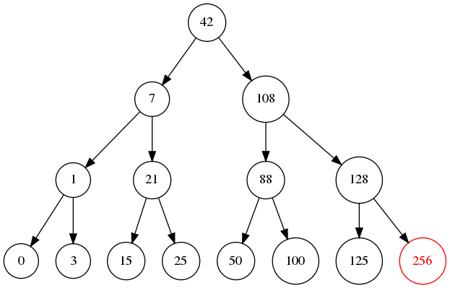
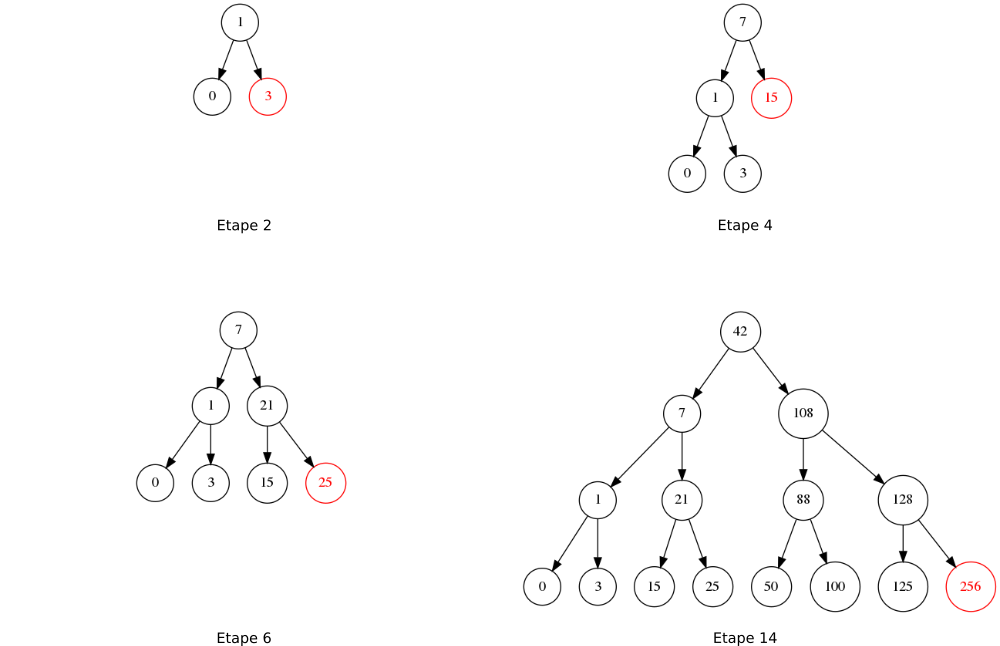
Dans un arbre rouge-noir, la recherche et l'insertion sont en
list.
from dataclasses import dataclass, field
from typing import Any, List
@dataclass
class Noeud:
"""Noeud d'un arbre n-aire."""
valeur: Any = None
descendants: List = field(default_factory=list)

 ) est caractérisé par :
) est caractérisé par :
 ).
). ).
). ) et un but (target
) et un but (target  ).
).
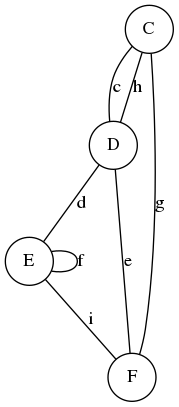
 ) ou graphe symétrique est caractérisé par :
) ou graphe symétrique est caractérisé par :
 |
 |
|---|---|
| Graphe orienté |
 |
 |
|---|---|
| Graphe orienté |
 |
 |
|---|---|
| Graphe orienté |
 |
 |
|---|---|
| Graphe simple |
 |
|---|
| Chemin |
 |
 |
|---|---|
| Chemin non simple | Chemin simple |
 |
 |
|---|---|
| Circuit | Cycle dans le graphe sous-jacent |
 |
 |
|---|---|
| Circuit non élémentaire | Circuit élémentaire |

 )
) |
 |
|---|---|
| DAG |
 |
 |
|---|---|
| Graphe simple | Fermeture transitive |
 |
 |
|---|---|
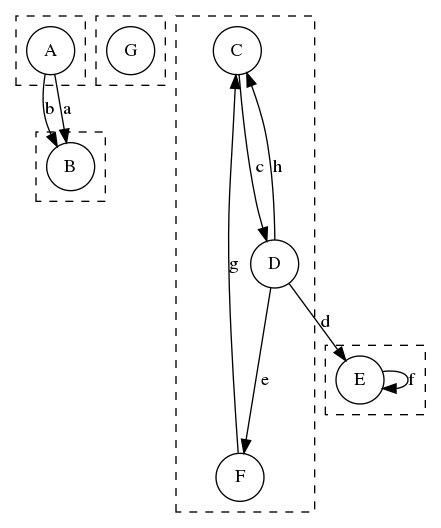
| Graphe non connexe | Graphe connexe |
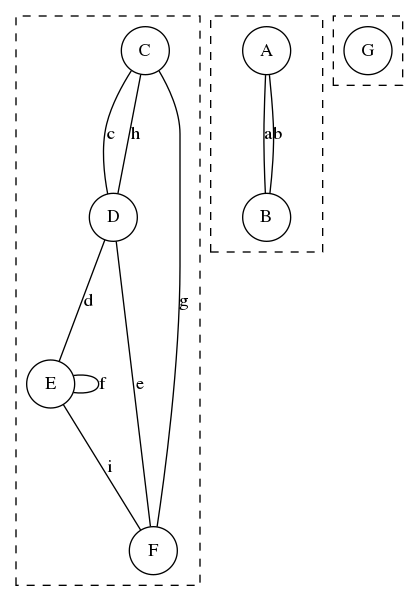
 |
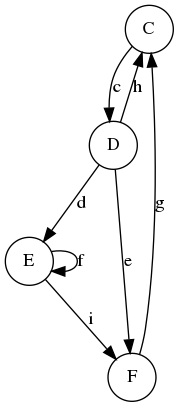 |
|---|---|
| Graphe non fortement connexe | Graphe fortement connexe |
G = [
[1], # 0 -> 1
[3, 4], # 1 -> 3, 1 -> 4
[4], # 2 -> 4
[0, 2], # 3 -> 0, 3 -> 2
[] # aucun
]
| sommets | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| sommet 0 : | 0 | 1 | 0 | 0 | 0 |
| sommet 1 : | 0 | 0 | 0 | 1 | 1 |
| sommet 2 : | 0 | 0 | 0 | 0 | 1 |
| sommet 3 : | 1 | 0 | 1 | 0 | 0 |
| sommet 4 : | 0 | 0 | 0 | 0 | 0 |
M = [
[0, 1, 0, 0, 0],
[0, 0, 0, 1, 1],
[0, 0, 0, 0, 1],
[1, 0, 1, 0, 0],
[0, 0, 0, 0, 0]
]
M = [
[None, "a", None, None, None],
[None, None, None, "b", "c"],
[None, None, None, None, "e"],
[ "f", None, "g", None, None],
[None, None, None, None, None]
]
| arêtes | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| sommet 0 : | 1 | 0 | 0 | 0 | 1 | 0 |
| sommet 1 : | 1 | 1 | 1 | 0 | 0 | 0 |
| sommet 2 : | 0 | 0 | 0 | 1 | 0 | 1 |
| sommet 3 : | 0 | 1 | 0 | 0 | 1 | 1 |
| sommet 4 : | 0 | 0 | 1 | 1 | 0 | 0 |
M = [
[1, 0, 0, 0, 1, 0],
[1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 1],
[0, 0, 1, 1, 0, 0]
]

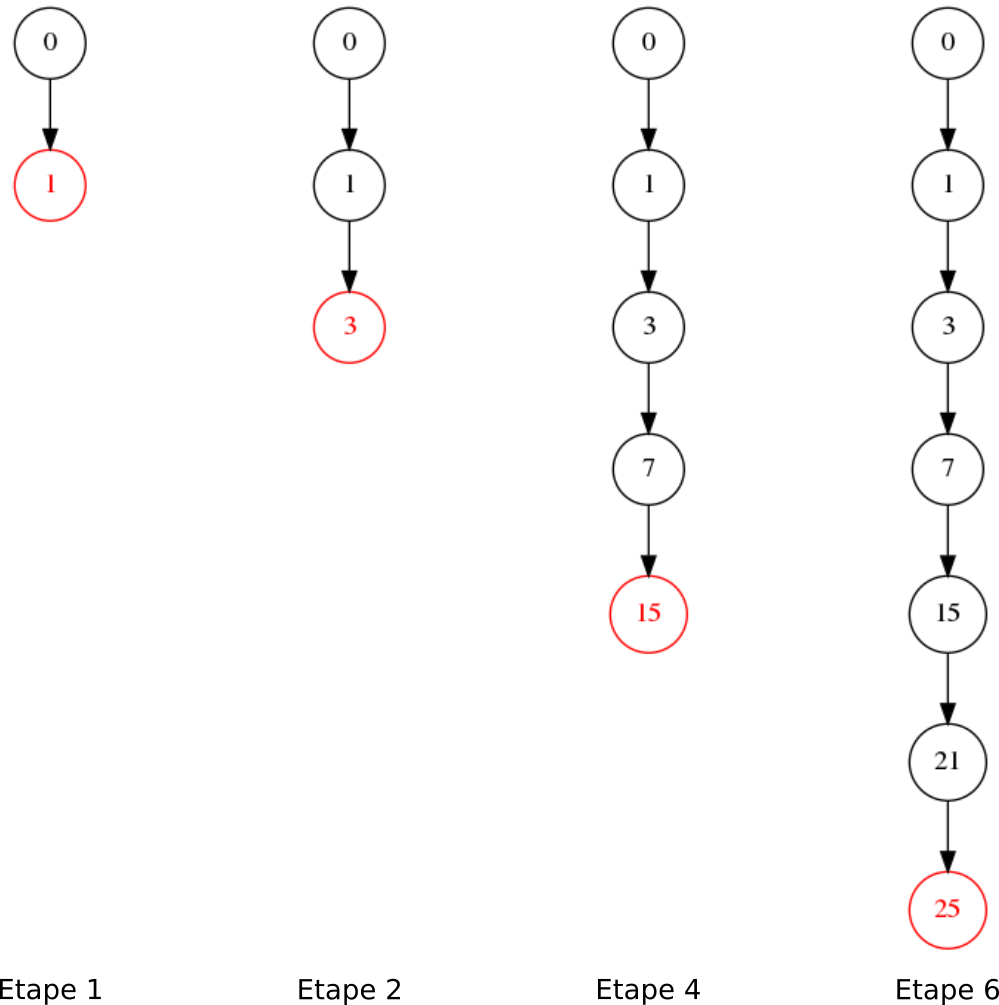
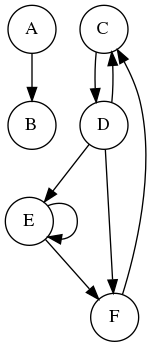
 ) consiste à aller aussi profondément que possible dans le graphe à chaque étape.
) consiste à aller aussi profondément que possible dans le graphe à chaque étape.
Ordre de visite : 0, 1, 4, 10, 11, 5, 6, 2, 7, 12, 13, 14, 3, 8, 9.

Ordre de visite : 0, 1, 3, 2, 4.

Ordre de visite : 0, 3, 2, 7, 12, 11, 6, 13, 14, 9, 10, 8, 4, 1, 5, 11, 15, 16, 17, 18, 19.
def parcours_en_profondeur(m, f):
"""Applique la fonction f à chaque sommet du graphe.
m - matrice d'adjacence.
f - fonction prenant un sommet en argument.
"""
def parcours_successeurs(m, s, f, marque):
"""Traitement récursif."""
if s not in marque:
marque.append(s)
f(s)
suivants = successeurs(m, s)
for suivant in suivants:
parcours_successeurs(m, suivant, f, marque)
marque = []
for s in range(len(m)):
parcours_successeurs(m, s, f, marque)

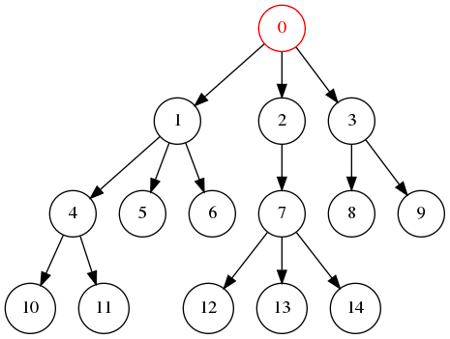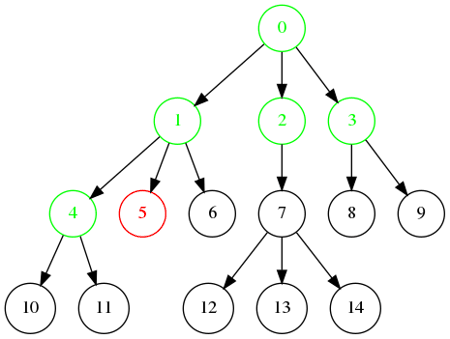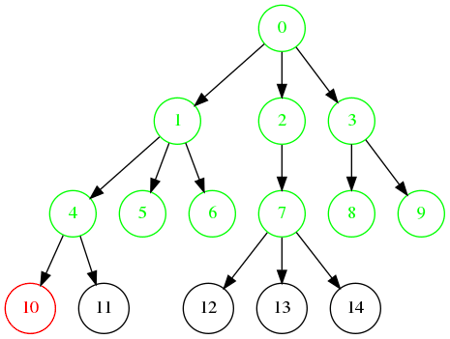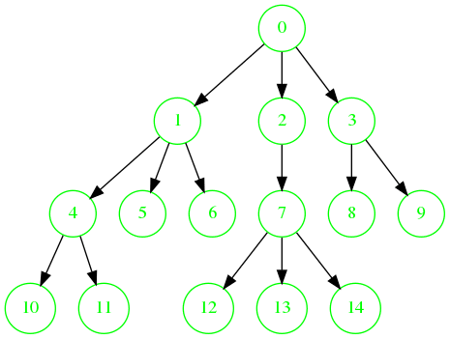
Ordre de visite : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
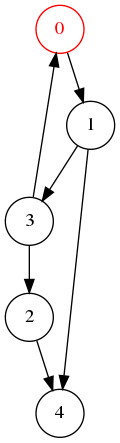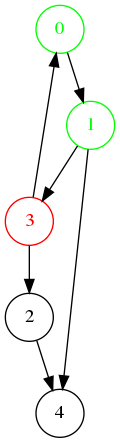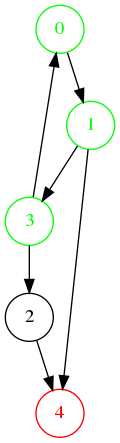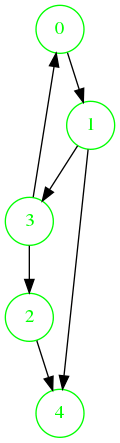
Ordre de visite : 0, 1, 3, 4, 2.

Ordre de visite : 0, 3, 4, 2, 8, 9, 1, 5, 11, 7, 6, 12, 13, 14, 10, 15, 16, 18, 17, 19.
def parcours_en_largeur(m, f):
"""Applique la fonction f à chaque sommet du graphe.
m - matrice d'adjacence.
f - fonction prenant un sommet en argument.
"""
marque = [] # On ne souhaite pas traiter plusieurs fois un sommet
queue = [] # On utilise une queue pour traiter d'abord les plus proches
for s in range(len(m)): # Visite chaque sommet pour les graphes non-connexes
if s not in marque: # Evite de traiter 2 fois un sommet
marque.append(s) # Marque le sommet courant à traiter
queue.append(s) # Empile dans la queue des sommets à traiter
while len(queue) != 0: # Tant que la queue est non vide
s_i = queue.pop(0) # On prend le 1er sommet
f(s_i) # On traite s_i
suivants = successeurs(m, s_i) # On prend les successeurs
for suivant in suivants: # On parcourt les successeurs
if suivant not in marque: # Les successeurs non marqués
marque.append(suivant) # sont marqués
queue.append(suivant) # et empilés.
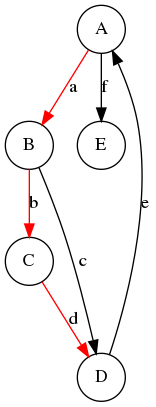
def cherche_cycle_en_profondeur(m, s, marque, chemin):
"""Recherche en profondeur un cycle.
m - matrice d'adjacence.
s - sommet à visiter.
marque - liste de sommets marqués.
chemin - chemin jusqu'à s.
"""
cs = chemin + [s] # On construit le nouveau chemin cs
if s in chemin: # Si un cycle est identifié dans le chemin,
return cs # on le renvoie.
if s not in marque: # Parcours en profondeur
marque.append(s) # On marque le sommet s
suivants = successeurs(m, s) # On prend les successeurs de s
for suivant in suivants: # On vérifie les sous-chemins
cycle = cherche_cycle_en_profondeur(m, suivant, marque, cs)
if cycle != None: # Si un cycle a été identifié dans
return cycle # un sous-chemin, on le renvoie.
return None # Pas de cycle identifié
def identifie_cycle(m):
"""Retourne le premier cycle identifié ou None."""
marque = []
for s in range(len(m)):
cycle = identifie_cycle_dans_chemin(m, s, marque, [])
if cycle != None:
return cycle
return None
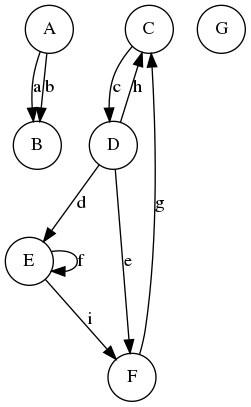
cycle = identifie_cycle(G)
print(cycle)
[0, 1, 3, 0]
G = [
[ # 0 -> 1 (poids = 42)
[1, 42]
],
[ # 1 -> 3 (poids = 21), 1 -> 4 (poids = -56.7)
[3, 21],
[4, -56.7]
],
[ # 2 -> 4 (poids = 7)
[4, 7]
],
[ # 3 -> 0 (poids = 3.14), 3 -> 2 (poids = -8)
[0, 3.14],
[2, -8]
],
[] # aucun
]
| sommets | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| sommet 0 : | 42 | ||||
| sommet 1 : | 21 | -56.7 | |||
| sommet 2 : | 7 | ||||
| sommet 3 : | 3.14 | -8 | |||
| sommet 4 : |
M = [
[None, 42, None, None, None],
[None, None, None, 21, -56.7],
[None, None, None, None, 7 ],
[3.14, None, -8, None, None],
[None, None, None, None, None]
]
@dataclass
class Sommet:
"""Sommet d'un graphe."""
label: int = 0
@dataclass
class Arc:
"""Arc d'un graphe orienté"""
origine: int = 0
but: int = 0
poids: float = 0.
@dataclass
class GraphePondere:
"""Graphe orienté pondéré."""
sommets: List = field(default=list)
arcs: List = field(default=list)
s0 = Sommet(0)
s1 = Sommet(1)
s2 = Sommet(2)
s3 = Sommet(3)
s4 = Sommet(4)
a0 = Arc(origine=0, but=1, poids=42)
a1 = Arc(origine=1, but=3, poids=21)
a2 = Arc(origine=1, but=4, poids=-56.7)
a3 = Arc(origine=2, but=4, poids=7)
a4 = Arc(origine=3, but=2, poids=-8)
a5 = Arc(origine=3, but=0, poids=3.14)
G = GraphePondere(sommets=[s0, s1, s2, s3, s4],
arcs=[a0, a1, a2, a3, a4, a5])
 ).
).def adjacents(m, s):
"""Renvoie les arcs adjacents à s dans m."""
adj = []
for j in range(len(m[s])):
if m[s][j] != None:
adj.append(Arc(origine=s, but=j, poids=m[s][j]))
return adj
def recalcule_bellman_ford(m, s, dist_a, arc_vers, queue):
"""Recalcule la distance minimale en considérant les successeurs de s.
m - matrice d'adjacence pondérée.
s - sommet dans les successeurs sont considérés.
dist_a - liste des distances minimales aux autres sommets.
arc_vers - liste des arcs conservés pour aller à un sommet donné.
queue - queue pour le parcours en largeur.
"""
adj = adjacents(m, s)
for arc in adj:
w = arc.but
if dist_a[w] == None or dist_a[w] > dist_a[s] + arc.poids:
dist_a[w] = dist_a[s] + arc.poids
arc_vers[w] = arc
if w not in queue:
queue.append(w)
def bellman_ford_impl(m, s):
"""Implémentation de Bellman-Ford sans gestion de cycles négatifs.
m - matrice d'adjacence pondérée.
s - sommet de départ.
Renvoie la liste des distances aux autres sommets et la liste des
arcs constituant les plus courts chemins.
"""
dist_a = [None for _ in range(len(m))] # distances à l'infini
dist_a[s] = 0 # distance à lui-même
arc_vers = [None for _ in range(len(m))] # résultat
queue = [s]
while len(queue) != 0:
v = queue.pop(0)
recalcule_bellman_ford(m, v, dist_a, arc_vers, queue)
return dist_a, arc_vers
def bellman_ford(m, s):
"""Renvoie une matrice d'adjacence correspondant au shortest path
tree (SPT) et la liste des distances minimales."""
dist_a, arc_vers = bellman_ford_impl(m, s)
spt = [[None for _ in range(len(m))] for _ in range(len(m))]
for arc in arc_vers:
if arc != None:
spt[arc.origine][arc.but] = arc.poids
return spt, dist_a
Note : Nous omettons la recherche de circuit négatif pour simplifier l'implémentation.
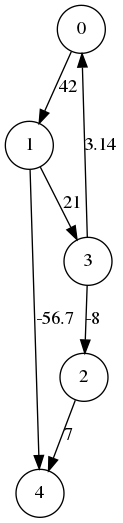 |
 |
|---|---|
| Graphe pondéré | Arbre de distances minimales pour |
Coûts = [0, 42, 55, 63, -14.7]
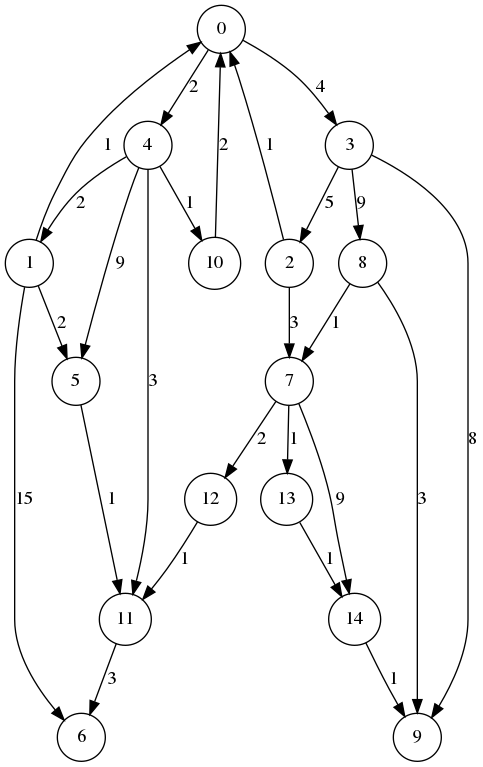 |
 |
|---|---|
| Graphe pondéré | Arbre de distances minimales pour |
Coûts = [0, 4, 9, 4, 2, 6, 8, 12, 13, 12, 3, 5, 14, 13, 14]
 ) utilise un DAG (graphe orienté acyclique) pour représenter et solutionner un problème d'ordonnancement.
) utilise un DAG (graphe orienté acyclique) pour représenter et solutionner un problème d'ordonnancement.| Tâches | Durée (jours) | Prédécesseurs |
|---|---|---|
| T1 : Architecturer Solution | 2 | |
| T2 : Configurer Serveurs | 1 | |
| T3 : Configurer BD | 3 | |
| T4 : Plan de Tests | 2 | |
| T5 : Coder Front End | 5 | T1 |
| T6 : Coder Backend | 7 | T1, T2, T3 |
| T7 : Tests | 3 | T4, T5, T6 |

NA = None # Non Applicable
M = [
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
[NA, 0, 0, 0, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA], # 0
[NA, NA, NA, NA, 2, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 1
[NA, NA, NA, NA, NA, 1, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 2
[NA, NA, NA, NA, NA, NA, 3, NA, NA, NA, NA, NA, NA, NA, NA, NA], # 3
[NA, NA, NA, NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA, NA, NA], # 4
[NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA, NA, NA, NA], # 5
[NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA, NA, NA, NA, NA, NA], # 6
[NA, NA, NA, NA, NA, NA, NA, NA, NA, 5, NA, NA, NA, NA, NA, NA], # 7
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 7, NA, NA, NA, NA, NA], # 8
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 9
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 10
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 2, NA, NA, NA], # 11
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0, NA, NA], # 12
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 3, NA], # 13
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0], # 14
[NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA] # 15
# 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
]
début à fin.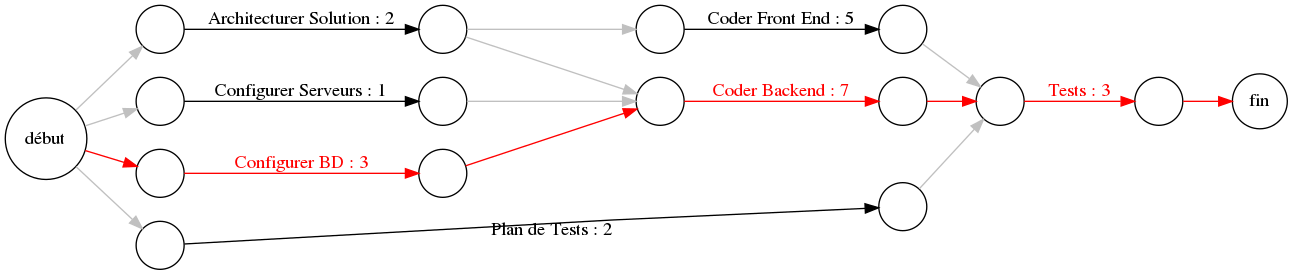
début à fin.2 devient donc un poids de -2 par exemple.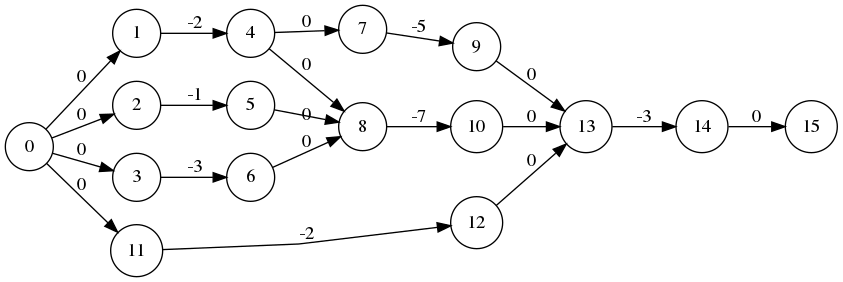
def oppose_poids(m):
"""Renvoie une matrice d'adjacence dont les poids sont opposés."""
resultat = []
for i in range(len(m)):
ligne = []
for j in range(len(m)):
if m[i][j] == None:
ligne.append(None)
else:
ligne.append(-m[i][j])
resultat.append(ligne)
return resultat
def chemin_vers(s, dist_a, arc_vers):
"""Renvoie le chemin vers le sommet s."""
if dist_a[s] == None:
return None
chemin = []
arc = arc_vers[s]
while arc != None:
predecesseur = arc.origine
chemin.insert(0, predecesseur)
arc = arc_vers[predecesseur]
return chemin
def chemin_critique(m):
"""Renvoie le chemin critique en utilisant PERT.
Utilise Bellman-Ford sur l'opposé de la matrice d'adjacence.
La matrice d'adjacence doit représenter un DAG.
Par convention, le début est supposé être le 1er sommer, et
la fin est supoosée être le dernier sommet.
"""
# Construit une matrice d'adjacence avec les poids opposés
m_p = oppose_poids(m)
# Calcule l'arbre des plus courts chemins
dist_a, arc_vers = bellman_ford_impl(m_p, 0)
# Le chemin vers la fin est le chemin critique
fin = len(m) - 1
chemin = chemin_vers(fin, dist_a, arc_vers)
return chemin
c = chemin_critique(M)
print(c)
[0, 3, 6, 8, 10, 13, 14]