Exemples d'autres problèmes
- Optimisation :
- Graphes, Tri, Recherche.
- Décision :
- Graphes, Tri, Recherche.
- Classification :
- Graphes, Tri, Recherche.
- Résolution d'équations (solver
)
| Famille d'algorithmes | Exemple de problème | Exemple d'algorithme |
|---|---|---|
| Recherche | Trouver un nombre dans une liste | Recherche binaire |
| Tri | Trier une liste | Tri Fusion |
| Graphes | Trouver le plus court chemin | Bellman-Ford |
| Chaînes de caractères | Trouver une sous-chaîne | Boyer-Moore |
 )
)inL = [1, 4, 8, 62]
if 4 in L:
print("On a trouvé 4")
On a trouvé 4
set et tupleS = {1, 4, 8, 62}
if 4 in S:
print("On a trouvé 4")
T = (1, 4, 8, 62)
if 4 in T:
print("On a trouvé 4")
On a trouvé 4
On a trouvé 4
Ch = "1, 4, 8, 62"
if "4" in Ch:
print("On a trouvé 4")
On a trouvé 4
D = {"un": 1, "quatre": 4, "huit": 8, "soixante deux": 62}
if "quatre" in D:
print("On a trouvé quatre")
if 4 in D.values():
print("On a trouvé 4")
On a trouvé quatre
On a trouvé 4
resultat = D.get("trois", -1)
print(resultat)
-1
def recherche_lineaire(collection, cle):
for i in range(len(collection)):
if collection[i] == cle:
return i
return -1
def recherche_lineaire(collection, cle):
def recherche_lineaire_impl(collection, cle, index):
if index == len(collection):
return -1
if collection[index] == cle:
return index
return recherche_lineaire_impl(collection, cle, index + 1)
return recherche_lineaire_impl(collection, cle, 0)

def recherche_binaire(collection, cle):
debut = 0
fin = len(collection) - 1
while debut <= fin:
milieu = debut + (fin - debut) // 2
actuel = collection[milieu]
if cle < actuel:
fin = milieu - 1
elif cle > actuel:
debut = milieu + 1
else:
return milieu
return -1



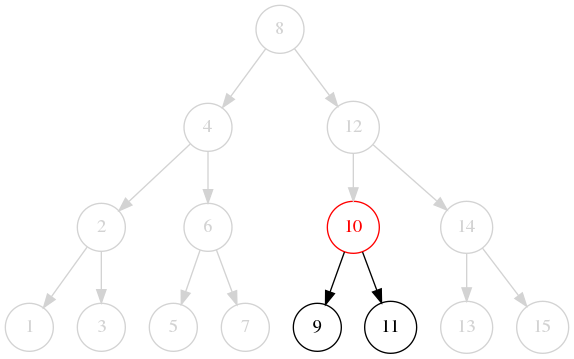


Donc le nombre total maximal de noeuds
On avait vu que la complexité de la recherche binaire était proportionnelle à la profondeur
def recherche_binaire(collection, cle):
def recherche_binaire_impl(collection, cle, debut, fin):
if fin < debut:
return -1
milieu = debut + (fin - debut) // 2
actuel = collection[milieu]
if cle < actuel:
return recherche_binaire_impl(collection, cle, debut, milieu - 1)
elif cle > actuel:
return recherche_binaire_impl(collection, cle, milieu + 1, fin)
else:
return milieu
debut = 0
fin = len(collection) - 1
return recherche_binaire_impl(collection, cle, debut, fin)

L = [6, 2, 5, 1, 9, 3, 8, 7, 4]
L.sort()
print(L)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
L1 = [6, 2, 5, 1, 9, 3, 8, 7, 4]
L2 = sorted(L1)
print(f"L1 = {L1}")
print(f"L2 = {L2}")
L1 = [6, 2, 5, 1, 9, 3, 8, 7, 4]
L2 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
T = (6, 2, 5, 1, 9, 3, 8, 7, 4)
T2 = sorted(T)
print(T2)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
S = {6, 2, 5, 1, 9, 3, 8, 7, 4}
S2 = sorted(S)
print(S2)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
Ch = "6, 2, 5, 1, 9, 3, 8, 7, 4"
Ch2 = sorted(Ch)
print(Ch2)
[' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
',', ',', ',', ',', ',', ',', ',', ',',
'1', '2', '3', '4', '5', '6', '7', '8', '9']
Ch = "6, 2, 5, 1, 9, 3, 8, 7, 4"
Ch3 = sorted(Ch.replace(" ", "").replace(",", ""))
print(Ch3)
['1', '2', '3', '4', '5', '6', '7', '8', '9']
D = {"un": 1, "deux": 2, "trois": 3}
D2 = sorted(D)
print(D2)
['deux', 'trois', 'un']
D = {"un": 1, "deux": 2, "trois": 3}
D3 = sorted(D.values())
print(D3)
[1, 2, 3]
L = [6, 2, 5, 1, 6, 9, 3, 8, 7, 4]
L.sort(reverse=True)
print(L)
[9, 8, 7, 6, 6, 5, 4, 3, 2, 1]
L = [(4, 3, 2, 1), [3, 2, 1], "ba"]
L.sort(key=len)
print(L)
['ba', [3, 2, 1], (4, 3, 2, 1)]
from dataclasses import dataclass
@dataclass
class paiement:
euros: int = 0
centimes: int = 0
L = [paiement(10, 0), paiement(3, 55), paiement(3, 99)]
L.sort(key=lambda x: (x.euros, x.centimes))
print(L)
[paiement(euros=3, centimes=55), paiement(euros=3, centimes=99),
paiement(euros=10, centimes=0)]
L = [paiement(10, 0), paiement(3, 55), paiement(3, 99)]
L.sort(key=lambda x: (x.euros, x.centimes), reverse=True)
print(L)
[paiement(euros=10, centimes=0), paiement(euros=3, centimes=99),
paiement(euros=3, centimes=55)]
from dataclasses import dataclass
@dataclass
class outil:
nom: str = ""
masse: float = 0.
L = [outil("marteau", 1.), outil("niveau", 0.5),
outil("cutter", 0.3), outil("compas", 0.3)]
L.sort(key=lambda x: (-x.masse, x.nom))
print(L)
[outil(nom='marteau', masse=1.0), outil(nom='niveau', masse=0.5),
outil(nom='compas', masse=0.3), outil(nom='cutter', masse=0.3)]
sort et sorted pour trier en Python. )
)def tri_selection(a):
N = len(a)
for i in range(N):
min = i
for j in range(i, N):
if a[j] < a[min]:
min = j
a[i], a[min] = a[min], a[i]
return a
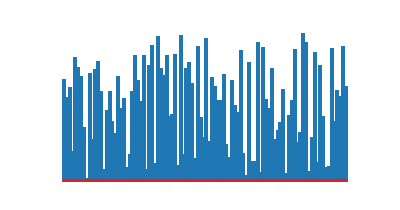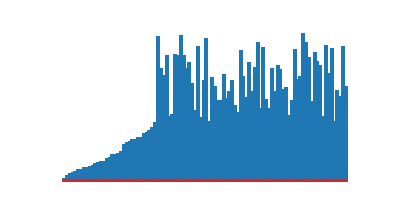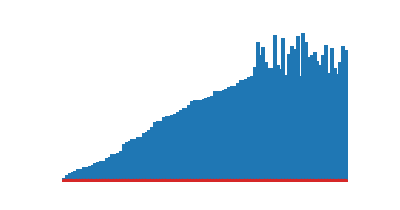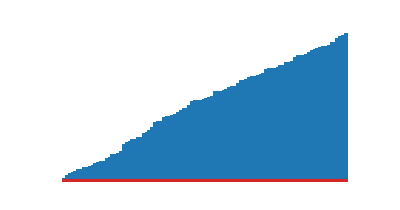
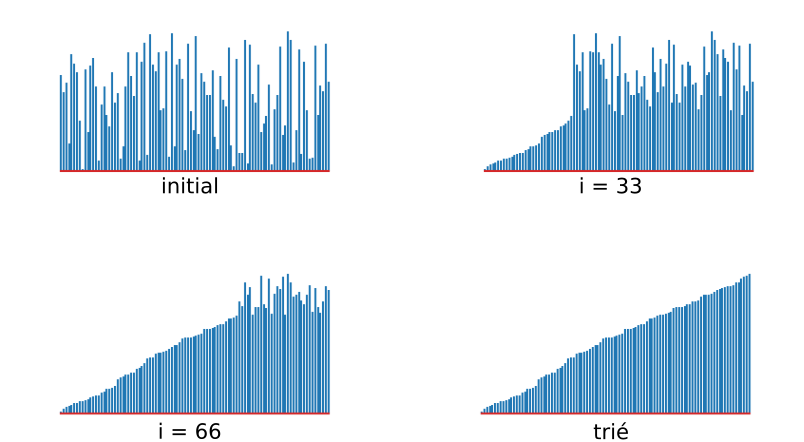
 )
)def tri_bulles(a):
N = len(a)
for i in range(N - 1):
for j in range(N - (i + 1)):
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
return a

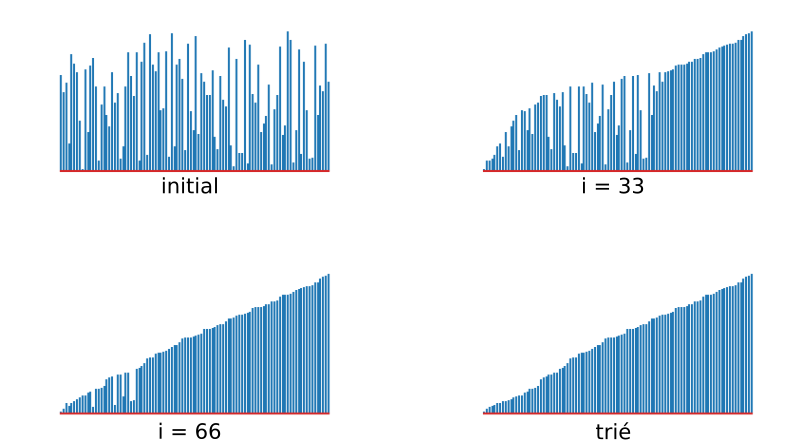
 )
)def tri_insertion(a):
N = len(a)
for i in range(1, N):
j = i
while j > 0 and a[j] < a[j-1]:
a[j], a[j-1] = a[j-1], a[j]
j -= 1
return a
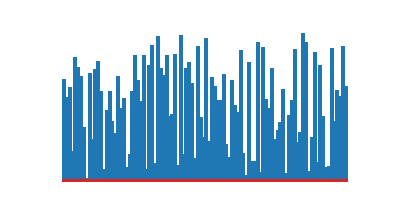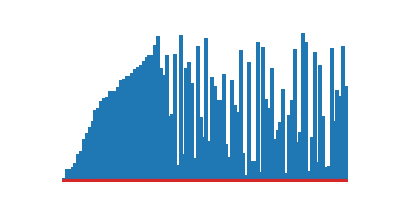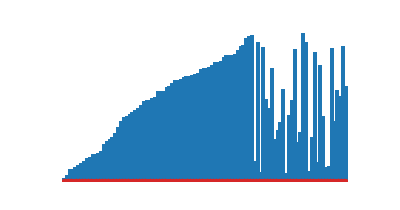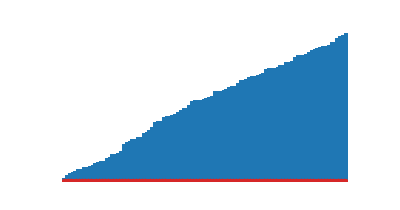
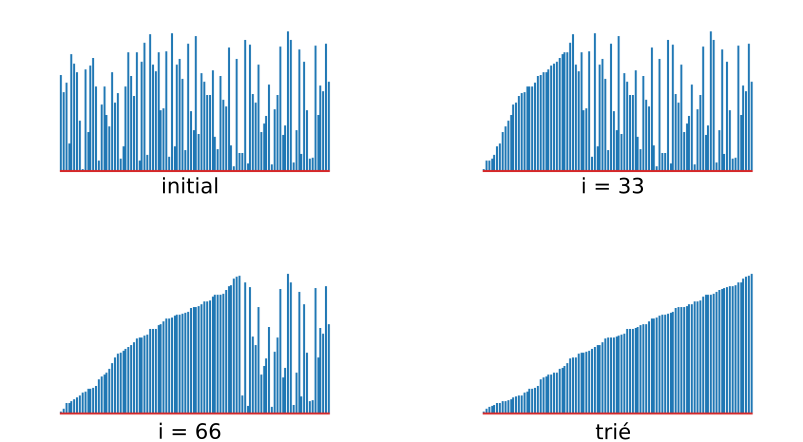
 )
)def tri_coquille(a):
N = len(a)
h = 1
while h < N // 3:
h = 3 * h + 1
while h >= 1:
for i in range(h, N):
j = i
while j >= h and a[j] < a[j-h]:
a[j], a[j-h] = a[j-h], a[j]
j -= h
h //= 3
return a
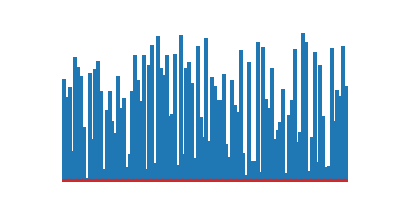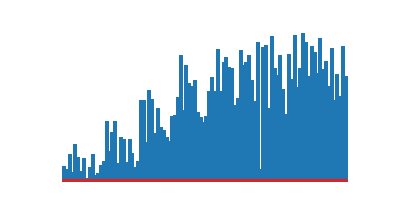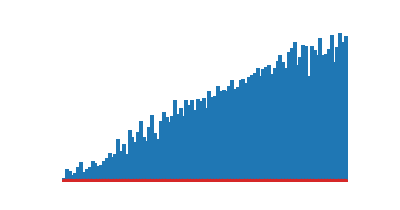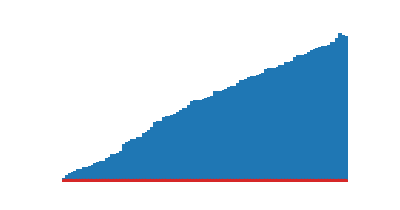

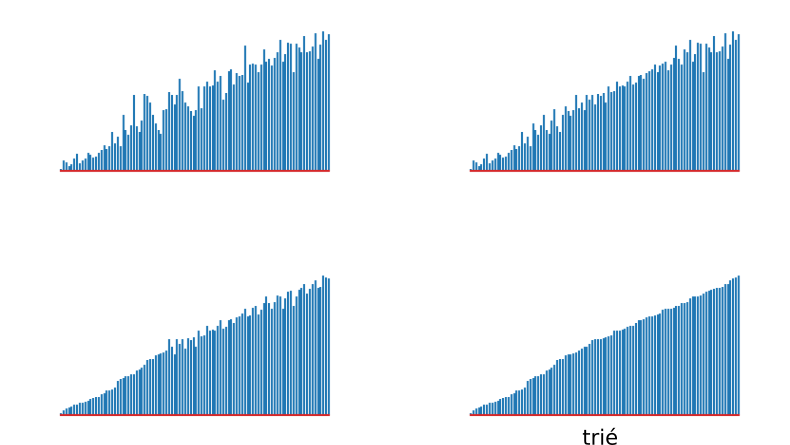
 |
 |
|---|---|
| Tri sélection | Tri à bulles |
 |
 |
|---|---|
| Tri sélection | Tri insertion |
 |
 |
|---|---|
| Tri insertion | Tri coquille |

def partition(e):
N = len(e)
valeur = e[0]
i = 0
j = N
while True:
i += 1 # Garanti la progression à droite
while e[i] < valeur and i != N: i += 1 # Scan vers la droite
j -= 1 # Garanti la progression à gauche
while valeur < e[j] and j != 0: j -= 1 # Scan vers la gauche
if i >= j: break # Si les indices se croisent on s'arrête
# Echange des éléments entre les 2 partitions
e[j], e[i] = e[i], e[j]
# Met la valeur de partitionnment entre les 2 partitions
e[j], e[0] = e[0], e[j]
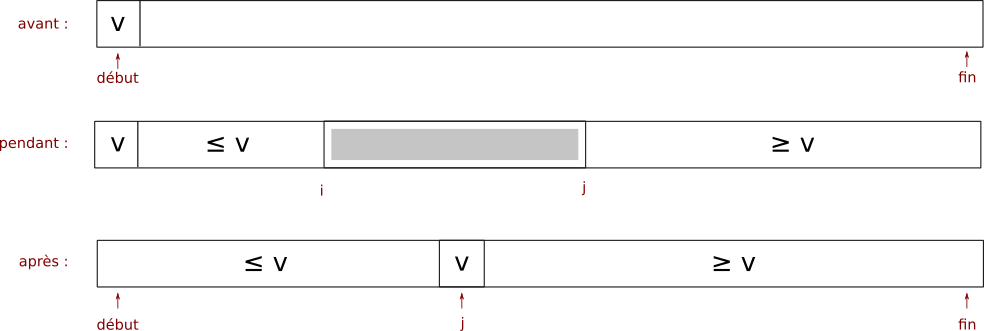
L = [6, 2, 5, 1, 9, 3, 8, 7, 4]
partition(L)
print(L)
[3, 2, 5, 1, 4, 6, 8, 7, 9]
L = [6, 2, 5, 1, 6, 9, 3, 8, 7, 4]
partition(L)
print(L)
[3, 2, 5, 1, 4, 6, 9, 8, 7, 6]

def partition(a, debut, fin):
i = debut
j = fin + 1
valeur = a[debut]
while True:
i += 1
while a[i] < valeur and i != fin: i += 1
j -= 1
while valeur < a[j] and j != debut: j -= 1
if i >= j: break
a[j], a[i] = a[i], a[j]
a[j], a[debut] = a[debut], a[j]
return j
 )
)def tri_rapide_recursif(a, debut, fin):
if fin > debut:
j = partition(a, debut, fin)
tri_rapide_recursif(a, debut, j - 1)
tri_rapide_recursif(a, j + 1, fin)
def tri_rapide(a):
N = len(a)
tri_rapide_recursif(a, 0, N - 1)

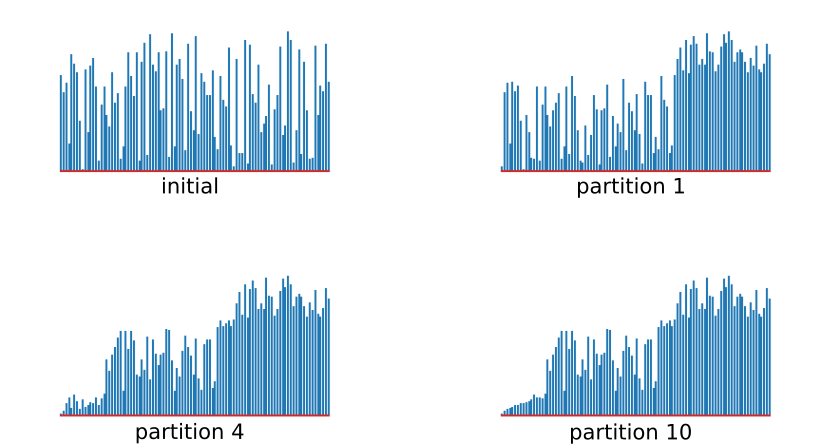

v ne se retrouve pas forcément au milieu.v se retrouve toujours en premier, cela signifie que la collection est déjà triée et le tri rapide sera lent et inutile.v se retrouve toujours exactement au milieu à chaque partitionnement.
def fusion(a, debut, milieu, fin):
i = debut
j = milieu + 1
auxiliaire = a[:]
for k in range(debut, fin + 1):
if i > milieu:
a[k] = auxiliaire[j]
j += 1
elif j > fin:
a[k] = auxiliaire[i]
i += 1
elif auxiliaire[j] < auxiliaire[i]:
a[k] = auxiliaire[j]
j += 1
else:
a[k] = auxiliaire[i]
i += 1
 )
)def tri_fusion_recursif(a, debut, fin):
if fin > debut:
milieu = debut + (fin - debut) // 2
tri_fusion_recursif(a, debut, milieu)
tri_fusion_recursif(a, milieu + 1, fin)
fusion(a, debut, milieu, fin)
def tri_fusion(a):
N = len(a)
tri_fusion_recursif(a, 0, N - 1)
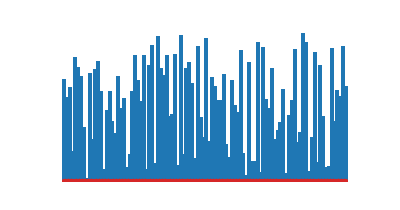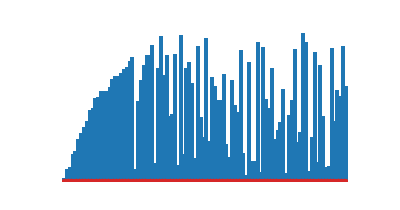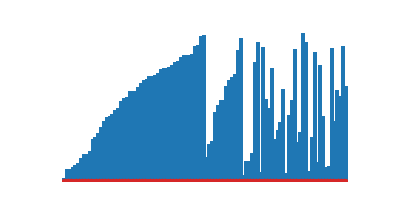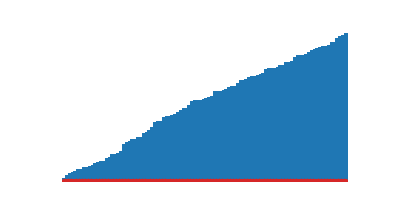


 |
 |
|---|---|
| Tri rapide | Tri fusion |